-
CRISTALOGRAFÍA
3.1. INTRODUCCIÓN
La mayoría de materiales sólidos poseen una estructura cristalina, conformada por el arreglo interno de sus átomos. La descripción de un sólido cristalino es por medio de las redes de Bravais, que especifica cómo las unidades básicas que lo componen (átomos, grupos de átomos o moléculas) se repiten periódicamente a lo largo del cristal.
El presente capítulo tiene como objetivo conocer la definición de cristalografía, algunos tipos de planos cristalinos, sus densidades volumétricas, lineales y planares, lo que es el factor de empaquetamiento, entre los diferentes tipos de estructuras cristalinas, se hará un reconocimiento de la aplicación de la técnica de difracción de rayos x y su función, así como también se definirán las imperfecciones cristalinas y sus diferentes tipos.
3.1.1. Cristalografía
La cristalografía es una ciencia que se ocupa del estudio de la materia cristalina, de las leyes que gobiernan su formación, y sus propiedades geométricas, químicas, y físicas.
Esta ciencia se clasifica en:
- Cristalografía geométrica; en esta clase de cristalográfica se estudia:
- La morfología externa de los cristales.
- La geometría y simetría de las redes cristalinas.
- Cuando se trata la materia cristalina desde un punto de vista macroscópico hay que considerarla como un medio homogéneo o continuo, anisótropo y simétrico.
- Cuando se estudia la simetría interna, es decir a nivel microscópico hay que considerar la materia cristalina como un medio homogéneo y discreto, además de isótropo y simétrico.
- Cristalografía química o cristaloquímica: en esta, se estudia la disposición de los átomos en la materia cristalina, es decir, se analiza con mayor rigor su estructura, por tal motivo se introduce el concepto de cristal real, en el cual se tienen en cuenta las imperfecciones, diferenciándose en esta parte de lo que se considera en la cristalografía geométrica.
- Cristalografía física o cristalofísica; se estudian las propiedades físicas de los cristales intentando relacionarlas con la composición química y la estructura.
Propiedades importantes a considerar. En esta parte son las que derivan de la interacción de la radiación X con la materia, ya que ellas permiten conocer la disposición de los átomos en la estructura, identificar fases cristalinas, etc.
Las partículas de los cuerpos sólidos, salvo excepciones, se ordenan en el espacio de acuerdo a determinados tipos de redes geométricas, también llamadas redes cristalinas. Este orden, que da a los sólidos su consistencia y la mayor parte de sus propiedades, constituye el campo de estudio de la cristalografía.
3.1.2. Formación de cristales
Cristal:
puede ser cualquier solido compuesto por moléculas, átomos o iones, y que sigue un patrón repetitivo y ordenado, a lo largo de las tres dimensiones espaciales.
Los sólidos cristalinos tienden a adoptar estructuras internas geométricas basadas en líneas rectas y planos paralelos.
Los componentes de los sólidos pueden ser de cuatro tipos:
- Átomos: partículas elementales de materia con carga eléctrica neutra.
- Iones: átomos con carga eléctrica negativa (aniones) o positiva (cationes) debidos a la transferencia o recepción, respectivamente, de uno o más electrones.
- Grupos iónicos: agrupación de varios iones de los mismos o diferentes elementos químicos.
- Moléculas: agrupación de varios átomos del mismo o de diferentes elementos.
3.1.3. Algunos conceptos cristalográficos
Estado cristalino:
Es el estado de equilibrio termodinámico de un sólido bajo unas condiciones termodinámicas (P, T) y con una composición determinada que corresponde a una determinada estructura cristalina.
Estructura cristalina:
Es la disposición periódica y ordenada en el espacio de tres dimensiones de los constituyentes atómicos de un sólido en estado cristalino.
Ejemplo: la halita, es un tipo de mineral que se forma por la evaporación de agua salada en algunos depósitos, esta posee un sistema cubico (Figura 3.1).
 Figura 3.1 Halita, tipo de mineral cristalino [3]
Figura 3.1 Halita, tipo de mineral cristalino [3]
NOTA: La principal propiedad de los sólidos en estado cristalino es la periodicidad, de la que se derivan otras características macroscópicas que son la: homogeneidad, anisotropía y simetría, como anteriormente se mencionaba en cristalografía geométrica.
Celda unidad:
Es una subdivisión de la red cristalina que conserva las mismas características y propiedades generales de toda red.
Sistema cristalino:
Es la forma geométrica de la celda unidad.
 Figura 3.3 Ejemplos de los sistemas cristalinos [4].
Figura 3.3 Ejemplos de los sistemas cristalinos [4].
Homogeneidad:
Desde el punto de vista macroscópico, significa, invariabilidad de una propiedad F medida en un punto X, en relación a su medida en otro punto X + X’, es decir:
F(x) = F ( x +x’)
Ecuación 3.1.
De la condición de la homogeneidad se obtiene, a nivel macroscópico, la constancia de la composición química y estado de fase a través de todo el volumen de la sustancia en estado cristalino.
El concepto de homogeneidad hace que se pueda considerar a una sustancia en estado cristalino como un continuo.
Este concepto es muy importante en cristalografía ya que se pueden dar descripciones fenomenológicas de muchas propiedades físicas de los cristales sin hacer referencia en su estructura atómica discreta. Cuando se consideran las propiedades físicas de los cristales a nivel macroscópico, se tratan con distancias considerables mayores que el espacio interplanar y con volúmenes que exceden con mucho el de la celda unidad.
Isotropía:
Existen ciertas propiedades de los cristales que son independientes de la dirección en la que se miden; se dice que son propiedades escalares, como el peso específico, la capacidad calorífica, entre otros.
Si la descripción de una propiedad es independiente de cualquier orientación, se dice que la sustancia es isótropa respecto a esa propiedad, respecto a lo tratado, se dice que un material es isótropo si su sistema cristalino no cambia, al variar su temperatura, presión.
Anisotropía:
existen otras propiedades que dependen de la dirección en la que se miden; de algunas se dice que son propiedades vectoriales, y de otras, tensoriales, como la conductividad térmica, la constante dieléctrica, el índice de refracción, etc.
Si una propiedad es dependiente de la orientación, se dice que la sustancia es anisótropa para dicha propiedad. En cualquier caso, una sustancia en estado cristalino siempre será anisótropa para alguna propiedad, como puede ser la diferente disposición de los átomos a lo largo de distintas direcciones (anisotropía estructural). [5]
Figura 3.4 Diferencia entre isotropía y anisotropía.
Polimorfismo:
Se define el polimorfismo como la posibilidad de que en un determinado elemento o compuesto químico pueda cristalizar según estructuras distintas. Las sustancias que así se comportan se denominan polimorfas.
El adoptar una u otra forma depende primordialmente de las condiciones de presión y temperatura que regían en el ambiente durante su formación.
En los polimorfos en que una de las especies cristalinas pasa rápidamente a otra modificación polimórfica cuando se rebasa un cierto límite la temperatura, se dice que la primera es meta estable (diamante) y la segunda estable (grafito), efectivamente, el grafito es la forma estable a presiones y temperaturas bajas. Se puede convertir en diamante aumentando la temperatura y la presión, y utilizando un catalizador para aumentar la velocidad.
En los casos de los átomos de carbono, además de formar el diamante según las características estructurales que han sido descriptas, dicho elemento químico es también constituyente de otra especie cristalina, un polimorfo del diamante es el grafito.
NOTA: Cuando hay dos más estructuras cristalinas diferentes para el mismo material se denomina polimorfismo o alotropía.
En la figura que a se muestra a continuación se dan algunos ejemplos de elementos, metales puros que son alotrópicos.
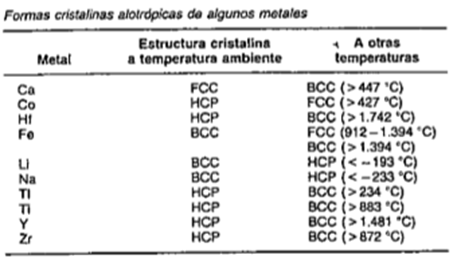 Figura 3.5 Ejemplos de metales puros que son alotrópicos.
Figura 3.5 Ejemplos de metales puros que son alotrópicos.
Simetría:
Es la propiedad que hace que un objeto no se distinga de su posición original después de haberle aplicado una transformación.
Teniendo en cuenta estas características, a nivel macroscópico, podemos definir a una sustancia en estado cristalino como un medio: homogéneo continuo, anisótropo y simétrico.
Sin embargo como se verá más adelante, una sustancia en estado cristalino no es un ente estático, ya que los átomos vibran y lo hacen en mayor grado cuando aumenta la temperatura. Esto afecta sus propiedades físicas. Muestra defectos y variaciones locales de su composición y también una desviación de la estructura respecto de la ideal. Estas imperfecciones no se consideran cuando se trata del medio cristalino desde un punto de vista macroscópico.
Habrá sustancias cuyas propiedades sean poco sensibles a defectos estructurales y puedan ser descritos utilizando un modelo de cristal ideal; en otras habrá que considerar su estructura real, ya que presentan propiedades que dependerán en mayor o menor extensión de los defectos estructurales.
Agregado cristalino:
Se define como un grupo de cristalitos (cristales de tamaño pequeño) que crecen juntos. Pueden aparecer con diversas formas. Algunos agregados cristalinos homogéneos son:
- Maclas: están formadas por dos o más cristales que, entre sí, presentan una simetría determinada por un eje o un plano de macla. Existen diferentes tipos de maclas: maclas de contacto, maclas de compenetración y maclas múltiples.
Figura 3.6. Maclas.
- Agregados Botroidales: son agregados homogéneos, formados por cristales de un solo mineral, que crecen en forma radial, constituyendo grupos esféricos arriñonados, muy característicos.
 Figura 3.7 Agregados botroidales.
Figura 3.7 Agregados botroidales.
- Agregados Dendríticos: están formados por cristales de un solo mineral, cuyos cristales crecen formando ramas divergentes, que similares a los fósiles de las plantas.
 Figura 3.8 Agregados dendríticos.
Figura 3.8 Agregados dendríticos.
- Drusas: son agregados homogéneos formados por cristales de un solo mineral, que crece sobre una superficie, plana o convexa.
- Geodas: están formadas por cristales de un solo mineral, que se encuentran tapizando una superficie cóncava, rellenan una cavidad.
[6]
3.1.4. Mineral:
Es aquella sustancia sólida, natural, homogénea, de origen normalmente inorgánico, de composición química definida (pero variable dentro de ciertos límites) y cuyos átomos poseen una disposición ordenada. La clasificación de Strunz es un método generalmente aceptado para clasificar los minerales.
En muchos casos desarrollan superficies planas conocidas como caras. Si el mineral ha sido capaz de crecer sin interferencias, pueden generar formas geométricas características, conocidas como cristales. [14]
3.1.4.1. Clasificación de los minerales:
Los minerales son sustancias compuestas de uno o varios elementos químicos y son ordenados en grupos según su composición química y su estructura, por tanto los minerales se pueden dividir en nueve clases principales:
Tabla 3.11 Clasificación de los minerales por composición química.
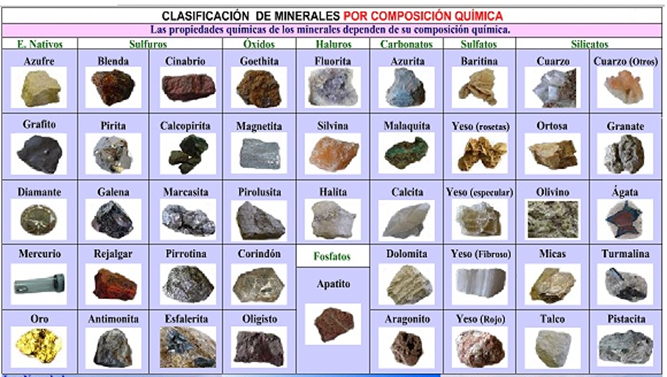 Figura 3.12 Clasificación de los minerales por composición química.
Figura 3.12 Clasificación de los minerales por composición química.
NOTA: La clasificación de los minerales se puede realizar de diferentes maneras, por composición química o por escala de dureza, a continuación se muestra en la figura otra clasificación de los minerales.
La escala de Mohs fue creada para comparar la dureza de los minerales, en la escala cada mineral puede rayar al anterior y a él mismo. La escala se llama así porque el geólogo que propuso que la hicieran, su apellido era Mohs.
3.1.4.2. Importancia de los minerales en el mundo:
Los minerales tienen gran importancia por sus múltiples aplicaciones en los diversos campos de la actividad humana. La industria moderna depende directa o indirectamente de los minerales; se usan para fabricar múltiples productos de la moderna civilización. Así, de distintos tipos de cuarzo y silicatos, se produce el vidrio. Los nitratos y fosfatos son utilizados como abono para la agricultura. Ciertos materiales, como el yeso, son utilizados profusamente en la construcción. Los minerales que entran en la categoría de piedras preciosas o semipreciosas, como los diamantes, topacios, rubíes, se destinan a la confección de joyas. [13]
Los minerales son un recurso natural de gran importancia para la economía de un país, muchos productos comerciales son minerales, o se obtienen a partir de un mineral. Muchos elementos de los minerales resultan esenciales para la vida, presentes en los organismos vivos en cantidades mínimas. [7]
3.1.4.3. Aplicación de los Minerales:
Los minerales tienen un sinfín de aplicaciones que abarcan los más variados campos de la actividad humana. La principal es, sin duda, la de constituir la fuente de obtención de los diferentes metales, base tecnológica de la moderna civilización. Así, de distintos tipos de cuarzo y silicatos, se produce el vidrio; el grafito, para las minas de lápices. Mezclas de minerales se producen componentes para computadoras. Los minerales que entran en la categoría de piedras preciosas o semipreciosas, como los diamantes, topacios, rubíes, se destinan a la confección de joyas. Los nitratos y fosfatos son utilizados como abono para la agricultura. Por último ciertos materiales, como el yeso, son utilizados profusamente en la construcción. [8]
3.1.4.4. Tipos de cristales.
3.1.4.4.1. Monocristal:
Se define como cristal único. Es decir, es cuando el arreglo del solido cristalino es perfecto. Esto implica que todas las celdas unitarias están bien definidas, unidas de la misma forma y siguiéndola misma orientación.
Ejemplo: a continuación se muestra en las figuras 3.14 y 3.15 dos monocristales, el primero que se observa es monocristal de calcita y el segundo constituye un monocristal de granate.
 Figura 3.14 Monocristal de Calcita
Figura 3.14 Monocristal de Calcita
Figura 3.15 Monocristal Granate.
Crecimiento de materiales monocristalinos:
- Método Clavier.
- Método Bridgman-Stockbarger.
- Método de Czochralski.
- Solidificación direccional.[10]
Aplicaciones más importantes de ingeniería de monocristales:
Tal vez una de las aplicaciones más importantes en la ingeniería es en la construcción de alabes para turbinas de gas, tal como se muestra en la figura a continuación.
En la década 1970-1980 comenzó la fundición de aleaciones monocristalinas, basadas en níquel, con aumento notable de resistencia y durabilidad térmica de los álabes de la turbina de gas. Soportan altas temperaturas de trabajo y aumentan la eficiencia térmica de la turbina. El ciclo termodinámico es el de Brayton Cycle. Los álabes de la turbina pueden ser policristalinos o monocristalinos. La forma pluricristalina se puede lograr mediante pulvimetalurgia, o por tecnología de fundición, colada en un molde de cerámica. Para el álabe con estructura monocristal, grano columnar, sirve la solidificación direccional, con paredes de granos paralelos a los ejes principales de esfuerzo, con aumento a la resistencia a la fluencia. No existen límites de grano en el material.
En la superaleación monocristal se usan muchos metales, además del níquel: Cr, Co, W, Mo, Ta, Ti, Al y Hf. Ahora se usa la 4ª generación de superaleaciones, difíciles de mecanizar y soldar, con mayores índices de rechazo. El monocristal carece de límites de grano en la dirección del eje, e impide la deformación del álabe.
La superaleación de base níquel con mayor endurecedor precipitado consiste en una matriz gamma y un precipitado intermetálico de gamma prima, que es superior al 50% de la aleación. Esta fase aumenta la resistencia mecánica del álabe, al aumentar la temperatura, porque impide el movimiento de la dislocación, la deformación. Para fabricar el monocristal se usa el método Bridgman y la solidificación direccional del eje en el horno de la fundición, con molde cerámico y cera fundida. El molde se llena con la superaleación de níquel fundida, y se enfría muy lentamente, de modo que la interfase sólido-líquido sube en el molde muy despacio; al níquel se añaden nuevos elementos en porcentajes pequeños.
La parte superior del horno de fundición tiene una temperatura superior a la de fusión, y la superaleación entra en el horno muy lentamente. Así la interfase sólido/líquido avanza también lentamente. En el sólido los granos crecen como dendritas, o sea, columnas en una dirección. La dendrita se enfría, y el calor pasa a la zona líquida. Las dendritas quedan alineadas en posición vertical. Tenemos métodos para eliminar en el álabe los límites de grano. Cuando se termina la solidificación solamente un grano forma el álabe de la turbina, el monocristal.
A menudo es beneficioso para los límites de grano que la superaleación a base de níquel contenga carburos (o boro o zirconio), para mejorar la resistencia a la fluencia, la deformación del álabe.
Conviene revestir las superaleaciones, sometidas a altas temperaturas de trabajo y a una atmósfera corrosiva. Principalmente se usan dos tipos de revestimiento: el proceso de cementación en paquete y el recubrimiento en fase gaseosa.
NOTA: Las propiedades cambian con la dirección: anisotrópicos.
 Figura 3.16 Ejemplo de alabe de una turbina.
Figura 3.16 Ejemplo de alabe de una turbina.
3.1.4.4.2. Policristales:
Un policristal o material policristalino es un agregado de pequeños cristales de cualquier sustancia, a los cuales, por su forma irregular, a menudo se les denomina cristalitos o granos cristalinos. Muchos materiales de origen tanto natural (minerales y metales) como sintético (metales, aleaciones, cerámica, etcétera) son policristales.
Las propiedades de los policristales están condicionadas por las propiedades de los granos cristalinos componentes, tales como:
- Tamaño medio. Comúnmente varía entre 1 y 2 micrones («micras»), de símbolo μ, hasta unos cuantos milímetros, y en algunos casos hasta unos cuantos metros.
- Orientación cristalográfica de los granos. Si los granos están orientados caóticamente y son pequeños comparados con el policristal, en éste no se detecta anisotropía de las propiedades físicas, la cual es propia de monocristales.
- Estructura del borde de grano. Así mismo, si en el policristalino hay una predominante orientación cristalográfica de los granos, el policristal se denomina texturizado. En este caso existe anisotropía de las propiedades. Puesto que en los bordes de los granos hay dispersión de electrones de conductibilidad, fotones, frenaje de dislocaciones, etcétera, los bordes influyen esencialmente en las propiedades físicas, especialmente en las mecánicas de los policristales.
Los policristales se generan por cristalización, o por transformaciones polimórficas, o como resultado de aglomeración de polvos cristalinos. Son menos estables que los monocristales. Por lo tanto, al someter un policristal ha recocido prolongado se puede producir recristalización: crecimiento preponderante de unos cuantos granos a costa de otros, que culmina en formación de grandes bloques cristalinos.
A continuación se observa una de las aplicaciones de policristales, son paneles policristalinos de silicio.
 Figura 3.17 Ejemplo de paneles policristalinos de silicio [11].
Figura 3.17 Ejemplo de paneles policristalinos de silicio [11].
NOTA: Las propiedades pueden o no variar con la dirección, si los granos están orientados al azar serán isotrópicos, si los granos están texturizados serán anisótropos. [10]
REFERENCIAS
- R. Askeland “Ciencia e Ingenieria de los materiales”, 3rd ed., p.39. International Thomson Editores, Universidad de Missouri, 1998.
- F. Smith “FUNDAMENTOS DE LA CIENCIA E INGENIERIA DE LOS MATERIALES”, 3rd ed., p.78.University of Central Florida, 1998.
- Estructura cristalina halita; recuperado el 11/05/15 de http://www.foro-minerales.com/forum/viewtopic.php?p=67048
- Sistema cristalino, ejemplos de los seis sistemas cristalinos; recuperado el 11/05/15 de http://www.tecnoficio.com/docs/doc9.php
- Anisotropía, isótropos y anisótropo; recuperado el 11/05/15 de http://edafologia.ugr.es/optmine/intro/isoanis.htm
- Agregado cristalino: maclas, agregados botroidales, agregados dentríticos, drusas, geodas; recuperado el 11/05/15 de http://3-2010-4-2011.es.tl/AGREGADOS-CRISTALINOS.htm
- Clasificación de los minerales, grupos, descripción, ejemplos; recuperado el 12/05/15 de http://3-2010-4-2011.es.tl/CLASIFICACI%D3N-DE-INERALES.htm
- Aplicaciones de los minerales; recuperado el 12/05/15 de http://www.quimica.es/enciclopedia/Mineral.html
- Crecimiento de materiales monocristales; recuperado el 12/05/15 de https://prezi.com/lnxu_efbwed6/estructuras-monocristalinas-metalicas/
- Aplicaciones más importantes de ingeniería de monocristales; recuperado el 12/05/15 de http://www.interempresas.net/Quimica/Articulos/132895-Alabes-monocristal-de-turbina-a-1600-C.html
- Policristales de silicio; recuperado el 12/05/15 de http://images-of-elements.com/silicon.php
- Cristalografía y mineralogía; recuperado el 12/05/15 de http://ocw.uniovi.es/ocw/
- Importancia de los minerales en el mundo E. Hernández, “¿Qué es un Mineral?” Museo de Mineralogía, Universidad Autónoma de Madrid, recuperado el 14/03/12.
3.2 REDES DE BRAVAIS
El nombre de bravais viene del Físico y mineralogista francés. Profesor de física y de astronomía Auguste Bravais que estableció la teoría reticular, según la cual las moléculas de los cristales están dispuestas en redes tridimensionales. Esta teoría, que explica los fenómenos de simetría y anisotropía de las sustancias cristalinas, fue posteriormente demostrada gracias a la difracción por rayos X.
Las redes de bravais son una disposición infinita de puntos conformando una estructura bajo cierto grupo de traslaciones, en la mayoría de casos no se dan cambios bajo rotaciones o simetría rotacional. Estas hacen que desde todos los nodos de una red de bravais tengan la misma perspectiva de red, por esto se dice que los puntos de una red son equivalentes. La invariancia traslacional de la red de Bravais constituye su característica más importante.
Figura 3.18. Auguste Bravais.
Además las Redes de Bravais o celdas unitarias sonconsiderados paralelepípedos que constituyen la menor subdivisión de una red cristalina que conserva las características generales de toda la reticula, de modo que por simple traslación del mismo, puede reconstruirse el sólido cristalino completo.
Se puede definir una red de bravais aplicando 3 criterios:
- En una red de bravais todos los puntos son equivalentes; es decir, deben ser invariantes bajo rotaciones y traslaciones.
- Las redes de bravais deben poseer una cierta simetría mínima.
- Ante dos o más redes de bravais, la verdadera red de bravais es aquella más sencilla. [3]
3.2.1 Geometría de las redes de Bravais
Estructura algebraica conocida por grupos que tiene una secuencia ordenada, sus objetivos son entre otros la clasificación de los grupos, sus propiedades y sus aplicaciones.
Por la teoría de grupos se ha demostrado que solo existe una única red de bravais unidimensional (simple secuencia de nodos equidistantes entre sí), 5 redes bidimensionales paralelogramos (2D) y 14 modelos distintos de redes tridimensionales paralelepípedo (3D).
 Figura 3.19 Clasificación de retículos espaciales en sistemas cristalinos.
Figura 3.19 Clasificación de retículos espaciales en sistemas cristalinos.
Redes Unidimensionales:
La red unidimensional es elemental siendo ésta una simple secuencia de nodos equidistantes entre sí. En dos o tres dimensiones las cosas se complican más y la variabilidad de formas obliga a definir ciertas estructuras patrón para trabajar cómodamente con las redes.
Figura 3.20. red unidimensional.
Redes bidimensionales:
Redes cristalinas en dos dimensiones podemos formar todas las que queramos, pues la longitud de los vectores de traslación de la base o el ángulo que forman es completamente arbitrario. Sin embargo no todas serán redes de Bravais. Existen únicamente 5 posibles redes de Bravais en dos dimensiones.
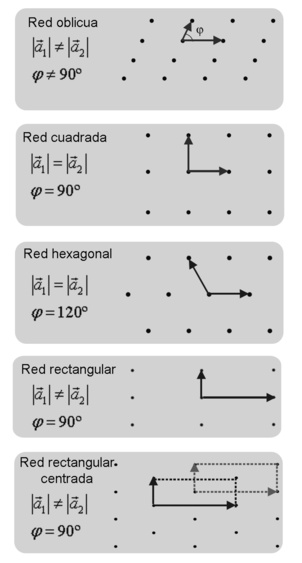 Figura 3.21 Redes bidimensionales.
Figura 3.21 Redes bidimensionales.
En la red oblicua tenemos una base en la que el módulo de los dos vectores es distinto. Además, el ángulo φ que forman no es de 90º.
Para le red cuadrada, el requisito que se debe de cumplir es que el módulo de ambos vectores sea el mismo y que el ángulo que formen sea recto, es decir 90º. Éste es el tipo de red más sencillo.
La red hexagonal tiene, como su propio nombre indica, una estructura de hexágonos y por tanto no tenemos un ángulo recto sino que el ángulo entre los vectores de la base es de 120º. Además, los módulos de ambos vectores deber ser iguales.
La red rectangular es una pequeña modificación de la red cúbica. En este caso, en lugar de tener los módulos de los dos vectores iguales, son diferentes. En cuanto al ángulo, obviamente sigue siendo de 90º.
Por último tenemos la red rectangular centrada. Es exactamente igual que la red rectangular, con los módulos de los vectores diferentes y un ángulo de 90º, pero con el añadido de contar con un punto extra en el centro del rectángulo. Se puede ver también como una red hexagonal con los módulos de los vectores distintos. De hecho, es así como se forma su celda primitiva.
Redes tridimensionales:
Para las redes de Bravais tridimensionales existen solamente siete grupos puntuales posibles y 14 grupos espaciales. Obviamente, varios grupos espaciales comportan el mismo grupo puntual. Esto permite clasificar todos los cristales en siete sistemas cristalinos (según el grupo puntual) y en 14 redes de Bravais (según el grupo espacial).
Las redes tridimensionales están formadas por la repetición de celdas unidad tridimensionales. Estas celdas vienen definidas por tres traslaciones: a, b y c, siendo a y b las traslaciones de la red plana, y c la traslación de dicha red plana en una dirección diferente (generalmente correspondiente al plano vertical).
Debido a la dificultad en el estudio de todas de estas redes vamos a indicar primero los 7 tipos diferentes que tenemos, y luego veremos algunas de las redes de Bravais más simples que son aquellas procedentes del sistema cúbico.
El sistema cúbico, como se puede ver en la figura 3.21 posee tres redes diferentes. Son las más sencillas de observar y son las que trataremos a continuación:
 Figura 3.22 Sistemas cúbicos cristalinos.
Figura 3.22 Sistemas cúbicos cristalinos.
[3]
En función de los parámetros de la celda unitaria, longitudes de sus lados y ángulos que forman, se muestran los 7 sistemas cristalinos.
Figura 3.23. relaciones lado angulo de los cristales. [4]
3.2.3 Densidad volumétrica.
Relación entre la masa de un cuerpo con respecto a su volumen. Basados en una celda unitaria, la densidad de un material puede ser hallada como:
Ecuación 3.2.
Utilizando el modelo de esferas rígidas para la estructura cristalina de la celda unidad de un metal, un valor de radio atómico del metal obtenido por análisis de difracción de rayos X se obtiene un valor de la densidad volumétrica del metal.
Para aplicar la fórmula mencionada debemos recordar los parámetros de red de las estructuras cristalinas presentes en los metales (BCC, FCC, HCP).
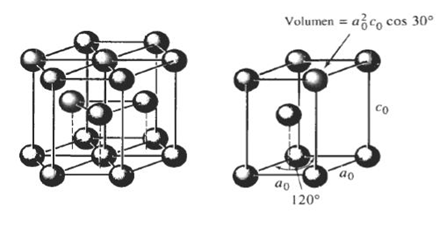 Figura 3.24 Estructuras HCP y tetragonal centrada en el cuerpo.
Figura 3.24 Estructuras HCP y tetragonal centrada en el cuerpo.
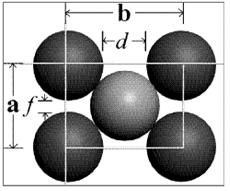 Figura 3.25. Estructura centrada, una cara.
Figura 3.25. Estructura centrada, una cara.
BCC: a = 4r/√3 volumen: a³
FCC: a = 4r/√2 volumen: a³
HCP: a = 2r c = [√ (2/3)]*4r volumen: (3/2)*√3*a²*c
Tabla 3.25. Características de las estructuras.
También podemos expresar esta ecuación de forma más general teniendo en cuenta que la masa celda unidad es:
(Número de átomos celda unidad) * (Peso molecular de los átomos)
Y volumen celda unidad es:
(Volumen celda unidad)*(Número de Avogadro)
Número de Avogadro = 6.02×1023 átomos/mol
El valor obtenido mediante ésta ecuación puede variar ligeramente del valor experimental consignado en tablas, lo cual debe atribuirse a la ausencia de algunas posiciones atómicas, defectos de línea, y uniones defectuosas entre los granos (límites de grano). Otra causa de esta situación puede deberse también a que los átomos no son esferas perfectas.
3.2.4 Ejemplos.
Ejemplo 3.1:
El cobre tiene una estructura cristalina FCC y un radio atómico de 0.1278 nm. Considerando a los átomos como esferas rígidas que se colocan entre sí a lo largo de la diagonal de la celda unitaria FCC, calcule el valor teórico de la densidad del cobre en mega metros por metro cubico. La masa atómica del cobre es de 63.54 g/mol.
Solución
Para la celda unitaria FCC, √2a =4R, donde a es la constante de red en la celda unitaria y R es el radio del átomo de cobre. Así:
a = 4R/√2 = (4*0.1278 nm)/√2 = 0.361 nm
Densidad volumétrica de un metal:
ρv = (Masa Celda unidad) / (Volumen celda unidad)
En la celda unitaria FCC hay cuatro átomos/celda unitaria. Cada átomo de cobre tiene una masa de (53.54 g/mol)*(6.02×1023 átomos/mol). Así, la masa m de los átomos de Cu en la celda unitaria es:
m = [(4 átomos)*(63.54 g/mol)/(6.02×10²³ átomos/mol)] * (10*10-6 Mg)/g
m = 4.22 * 10 -28 Mg
El volumen V de la celda unitaria del Cu es:
V = a³ = [0.361 nm * (10 -9 m)/nm]³
V = 4.70 * 10 -29 m³
Así la densidad del cobre es:
ρv = m/v = (4.22 * 10 -28 mg)/(4.70 * 10 -29) = 8.98 Mg/m³
Respuesta: ρv (cobre) = 8.98 Mg/m³
Ejemplo 3.2:
Determine la densidad del hierro BCC, cuyo parámetro de red es 0.2866 nm.
Solución
Para una celda BCC:
Átomos por celda = 2
a = 0.2866 nm.
Masa atómica = 55,847 g/mol
Volumen de la celda unitaria = a³ = (2.866 * 10 -8 cm)³ = 23.54 * 10 -24 cm³/celda
Número de Avogadro = NA = 6.02 * 10 ²³ átomos/mol
ρv = [número de átomos por celda * peso molecular de los átomos]/ [volumen de la celda unitaria * número de Avogadro]
ρv = (2*55.847) / (23.54* 10 -24 * 6.02 * 10 ²³) = 7.882 g/cm³
Respuesta: ρv (hierro) = 7.882 g/cm³
La densidad medida es 7.870 g/cm³. La pequeña discrepancia entre las densidades teórica y medida es una consecuencia de los defectos en el material. Como se dijo antes el término “defecto” en este contexto, significa imperfecciones respecto al arreglo atómico.
Ejemplo 3.3:
La plata tiene una estructura cristalina FCC con un radio atómico de 0.144 nm. Calcule el valor teórico de la densidad de la plata en g/cm³.
Solución
Masa atómica (Ag) = 107.87 g/mol
Masa = [(4 átomos * 107.87 g/mol) / (6.02 * 10²³ átomos/mol)]
Masa = 7.167 * 10-22 g
Volumen para una celda BCC = a³ donde a =4r/√2
Entonces tenemos:
Volumen en cm³ = [((4 * 0.144*10-9 m) / √2)*(100 cm / 1 m)]³
Volumen = 6.756 * 10–²³ cm³
Así la densidad teórica de la plata es:
ρv = m/v = 7.167 * 10-22 g / 6.756 * 10-23 cm³
Respuesta: ρv (plata) = 10.608 g/cm³
Ejemplo 3.4:
La densidad del torio que tiene una estructura FCC es de 11.72 g/cm³. El peso atómico del torio es de 232 g/mol. Calcule:
- El parámetro de red.
- El radio atómico del torio.
Solución
a. Como es una es una estructura FCC el parámetro de red a = 4r/√2 y el volumen de la celda es a³.
Utilizando:
ρv = [número de átomos por celda * peso molecular de los átomos] / [volumen de la celda unitaria * número de avogadro]
Tenemos:
11.72 g/cm³ = (4 átomos * 232 g/mol) / [(4r/√2)³ * 6.02*10²³ átomos/mol]
Despejando r:
r³ * 11.72 /cm³ = 928 / 1.36*10 25
r³ = 6.82*10–²³ cm³ / 11.72
Respuesta: r = 1.799*10-8 cm
b. Usando a = 4r/√2tenemos:
a = (4 * 1.799*10-8 cm) / √2
Respuesta: a = 5.088*10-8 cm
Ejemplo 3.5:
El bismuto tiene una estructura hexagonal, con a = 0.4546 nm y c = 1.186 nm. La densidad es 9.808 g/cm³ y el peso atómico es de 208.98 g/mol. Determine:
- El volumen de la celda unitaria.
- Cuantos átomos Existen en cada Celda unitaria.
Solución.
a. Mirando la figura de la celda hexagonal compacta y teniendo en cuenta que el volumen es la base multiplicada por la altura (c) y además descomponiendo esta base en 6 triángulos equiláteros, podemos llegar a la conclusión de que el volumen de la celda es:
V = (3/2)*√3*a²*c
Reemplazando tenemos:
V = (3/2) * √3 * (0.4546 nm)² *9.808 nm
Respuesta: V= 0.637 nm³
b. V = 0.637 nm³ = 0.637*10-²¹ cm³
Reemplazando todos los datos en
ρv = [número de átomos por celda * peso molecular de los átomos] / [volumen de la celda unitaria * número de Avogadro]
Y tomando como N = número de átomos tenemos:
9.808 g/cm³ = (N * 208.98 g/mol) / (0.637*10-²¹ cm³ * 6.02*10²³ átomos/mol)
Despejando N
Respuesta: N = 18 átomos
Ejemplo 3.6:
La densidad del potasio, que tiene una estructura BCC es 0.855 g/cm³. El peso atómico del potasio es 39.09 g/mol. Calcule:
- El parámetro de red.
- El radio atómico del potasio.
Solución
a. Sabemos que al ser una celda BCC tiene 2 átomos en su interior.
Reemplazando todos los datos otorgados en
ρv = [número de átomos por celda * peso molecular de los átomos] / [volumen de la celda unitaria * número de Avogadro]
Tenemos:
0.855 g/cm³ = [(2 átomos * 39.09 g/mol) / (a³ * 6.02*10²³ átomos/mol)]
Despejando a:
a³ = 1.519*10-²² cm³
Respuesta: a = 5.336*10-8 cm
b. a = 4r/√3
Despejando r:
r = [(5.336*10-8 cm) √3] / 4
Respuesta: r = 2.31*10-8 cm
3.2.5 Factor de empaquetamiento atómico (FEA)
En cristalografía, el factor de empaquetamiento atómico (FEA), en inglés: Atomic packing factor, APF , es la fracción de volumen en una celda unidad que está ocupada por átomos. Este factor es adimensional y siempre menor que la unidad. Para propósitos prácticos, el FEA de una celda unidad es determinado asumiendo que los átomos son esferas rígidas. Para cristales de un componente (aquellos que contienen un único tipo de átomo), el FEA se representa matemáticamente por:
Donde Nátomos es el número de átomos en la celda unidad, Vátomo es el volumen de un átomo, y Vcelda unidad es el volumen ocupado por la celda unidad. Matemáticamente puede ser probado que para estructuras de un componente, el arreglo más denso de átomos tiene un FEA alrededor de 0.74. En realidad, este número puede ser mayor debido a factores intermoleculares específicos. Para estructuras de múltiples componentes, el FEA puede exceder el 0.74.
Generalmente se acepta que la naturaleza favorece los arreglos y estados de la materia que tienden a minimizar los niveles de energía (energía potencial). Por ello podemos preguntarnos qué tan eficiente es en verdad el arreglo de un cristal y si es razonable asumir un empaquetamiento denso; para este último se realiza la convención de:
- Generalmente sólo está presente un elemento, por lo que todos los radios atómicos son iguales.
- El enlace metálico no es direccional.
- La distancia a los primeros vecinos tienden a ser cortas para disminuir la energía de enlace.
- La nube electrónica cubre a los núcleos.
Entonces, para evaluar la eficiencia de la estructura cristalina o cuán eficiente están arreglados los átomos se calculará el volumen atómico contenido en la celda unitaria en relación con el volumen total de la celda unitaria como sigue:
Es el porcentaje (%) que se encuentra ocupado por átomos el cristal. [7]
F.E = # equivalente de átomos en la celda * vol del átomo*100/vol total de la celda.
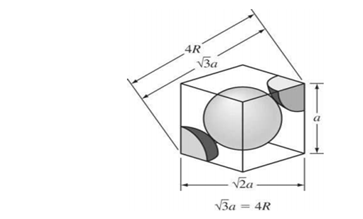 Figura 3.26 Arista de estructura BCC en función del radio atómico.
Figura 3.26 Arista de estructura BCC en función del radio atómico.
Ejemplo 3.7:
Calcule el factor de empaquetamiento atómico para la celda unidad BCC, considerando los átomos como esferas rígidas
Solución:
APF=Volumen de los átomos en la celda unidad BCC / Volumen de la celda unidad BCC
Puesto que tenemos dos átomos por celda unidad BCC, el volumen de los átomos de radio R en una celda unidad es,
Vátomos= (2) (4/3 Π R^3)
El volumen de la celda unidad es:
Vcelda unidad= a^3
Donde a es la constante de red. La relación entre a y R se obtiene a partir de la figura 3.25, que muestra cómo los átomos de la celda unidad contactan a través de la diagonal del cubo. Así,
√3 a=4R
Entonces:
Vcelda unidad= a^3=12,32 R^3
El factor de empaquetamiento atómico para la celda unidad BCC resulta ser,
REFERENCIAS
- Química, la ciencia central; quinta edición; “Prentice hall brown and burnstein.1993.”
- Fundamentos de la ciencia e ingeniería de materiales 4ta edición; “William F. Smith, Javad Hashemi”.
- http://fisica.laguia2000.com/fisica-del-estado-solido/estructura-cristalina-y-redes-de-bravais-ii; recuperado el 23/05/2015
- http://www.angelfire.com/la/SEMICONDUCTORES/concept.html; recuperado el 23/05/2015
- http://www.iim.unam.mx/mbizarro/3-2015Estructura%20cristalina%20de%20solidos%202013-2.pdf; recuperado el 23/05/2015
- http://mim-us.es/estructuras_cristalinas/planos.html; recuperado el 23/05/2015
- http://www.utp.edu.co/~publio17/temas_pdf/estructura_sol.pdf; recuperado el 23/05/2015
3.3 ÍNDICES DE MILLER
Estos se utilizan para identificar los planos cristalinos por donde es susceptible de deslizar unos átomos sobre otros átomos en la celda cristalina.
Para poder identificar unívocamente un sistema de planos cristalográficos se les asigna un juego de tres números que reciben el nombre de índices de Miller. Los índices de un sistema de planos se indican genéricamente con las letras (h k l)
Los índices de Miller son números enteros, que pueden ser negativos o positivos, y son primos entre sí. El signo negativo de un índice de Miller debe ser colocado sobre dicho número.
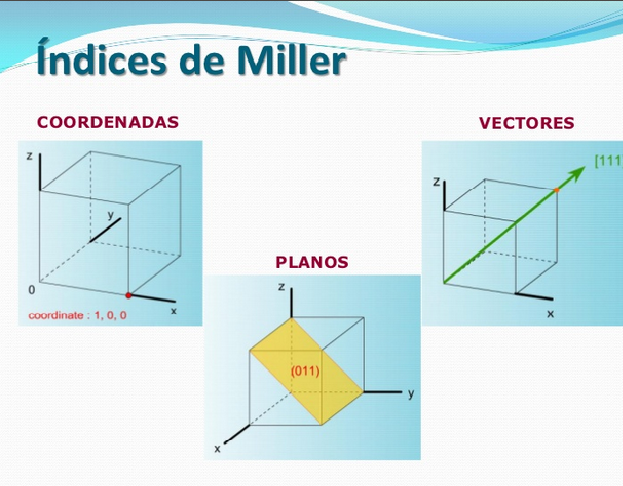 Figura 3.27. Representación en el espacio de planos, vectores y coordenadas.
Figura 3.27. Representación en el espacio de planos, vectores y coordenadas.
3.3.1. Ejes y celdas unitarias:
Se utilizan los tres ejes conocidos normalmente, el eje X positivo se usa saliendo del papel, el eje Y positivo hacia la derecha y finalmente el eje Z positivo hacia la parte superior; en sentidos opuestos se encuentran sus respectivas zonas y cuadrantes negativos
 Figura 3.28 Coordenadas espaciales en celdas unitarias cúbicas.
Figura 3.28 Coordenadas espaciales en celdas unitarias cúbicas.
Se utilizan celdas unitarias para situar tanto puntos, como planos. Dichas celdas unitarias son cubos los cuales se encuentran situados sobre el sistema de coordenadas X, Y, Z. Generalmente se asume un origen, el cual está ubicado en la arista inferior izquierda posterior.
 Figura 3.29 Coordenadas espaciales y aristas en celdas unitarias cúbicas.
Figura 3.29 Coordenadas espaciales y aristas en celdas unitarias cúbicas.
 Figura 3.30 Vértices o puntos de red de las celdas unitarias cúbicas.
Figura 3.30 Vértices o puntos de red de las celdas unitarias cúbicas.
3.3.2. Direcciones en la celda unitaria:
Existen direcciones y posiciones en una celda unitaria de gran interés, dichas direcciones son los denominados Índices De Miller y son particularmente las posiciones o lugares por donde es más susceptible un elemento en sufrir dislocaciones y movimientos en su interior cristalino.
Para hallar los Índices De Miller de las direcciones se procede de la siguiente manera:
- Usar un sistema de ejes coordenados completamente definidos (zonas positivas y zonas negativas).
- Restar las coordenadas de los puntos a direccionar (cabeza menos cola), generando de esta manera el vector dirección y la cantidad de parámetros de red recorridos
- Eliminar o reducir de la resta de puntos las fracciones hasta su mínima expresión
- Encerrar los números resultantes entre corchetes , sin comas, si el resultado es negativo en cualquier eje (X, Y, Z) debe situarse una barra o raya encima de dicho número, o números.
Ejemplo 3.8:
Determinar los índices de Miller de las direcciones A, B y C.
Dirección A
- Dos puntos son: 1,0,0 y 0,0,0
- Se restan ambos puntos, situando en primer lugar el punto que se desea tener como dirección y sentido (cabeza del vector) 1,0,0 – 0,0,0 = 1,0,0
- No existen fracciones que eliminar ni enteros que reducir
- [100].
Dirección B
Dos puntos son: 1, 1, 1 y 0, 0,0
- Se procede de igual manera, se restan ambos puntos 1,1,1 – 0,0,0 = 1,1,1
- No existen fracciones que eliminar ni enteros que reducir
- [111]
Dirección C
- Dos puntos son: 0,0,1 y ½,-1,0
- Se procede de igual manera, se restan ambos puntos 0,0,1 – ½,-1,0 = – ½,-1, 1
- Esta vez el resultado debemos llevarlo a una conversión de enteros.
- 2(- ½,-1, 1)=-1,-2,2
- Como el resultado es negativo en las direcciones de los ejes X y Y, se sitúan con una barra en la parte superior los valores para dichos ejes.
3.3.3. Aspectos importantes en el análisis y creación de las direcciones en los índices de Miller.
Las direcciones de Miller son vectores, por ende este puede ser positivo o negativo, y con ello poseer la misma línea de acción pero diferente sentido.
- Una dirección y sus múltiplos son idénticos solo que estos aún no han sido reducidos.
- Ciertos grupos de direcciones poseen equivalentes, esto en un sistema cubico es ocasionado por el orden y el sentido de los vectores, ya que es posible redefinir el sistema coordenado para una misma combinación de coordenadas. Estos grupos reciben el nombre de direcciones de una forma o familia, y se denota entre paréntesis especiales <>. Es importante resaltar que un material posee las mismas propiedades en todas y cada una de las diferentes direcciones de una familia.
Direcciones de la familia <100> en el sistema cúbico
 Figura 3.31 Direcciones de la familia <100> en el sistema cúbico.
Figura 3.31 Direcciones de la familia <100> en el sistema cúbico.
Direcciones de la familia <110> en el sistema cúbico
 Figura 3.32 Direcciones posibles de la familia <110>.
Figura 3.32 Direcciones posibles de la familia <110>.
Direcciones de la familia <111> en el sistema cúbico
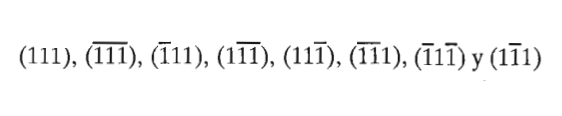 Figura 3.33 Direcciones de la familia <111> en el sistema cúbico
Figura 3.33 Direcciones de la familia <111> en el sistema cúbico
3.3.4. Importancia de las direcciones cristalográficas:
Es necesario conocer las direcciones cristalográficas para así asegurar la orientación de un solo cristal o de un material policristalino. En muchas ocasiones es necesario describir dichas orientaciones; en los metales por ejemplo es más fácil deformarlos en la dirección a lo largo de la cual los átomos están en mayor contacto. En la industria esto es de vital importancia para el uso, deformación y construcción de nuevos elementos y materiales. Caso ejemplar es el de los elementos magnéticos los cuales funcionan como medios de grabación con mejor y mayor eficiencia si se encuentran alineados en cierta dirección cristalográfica, para así almacenar de manera segura y duradera la información. En general es necesario encontrar o tener en cuenta la posición y dirección cristalográfica de los elementos ya que así podrá aprovecharse al máximo sus propiedades mecánicas.
3.3.5. Planos en la celda unitaria:
Los planos cristalinos son con mayor precisión los lugares por donde un material facilita su deslizamiento y transformación física; dichos lugares o planos son en donde existe la mayor posibilidad de que el elemento sufra una dislocación. Como se mencionó anteriormente los metales se deforman con mayor facilidad a lo largo de los planos en los cuales los átomos están compactados de manera más estrecha o cercana en la celda unitaria. Es importante resaltar la orientación y forma en la que puede crecer el cristal, para ello es necesario analizar las tensiones superficiales producidas en los principales planos de una celda unitaria. Igualmente para una mejor orientación en los planos de un material podrá existir un mejor rendimiento y aprovechamiento en las propiedades y usos mecánicos.
Para identificar los planos cristalinos en una estructura cristalina cubica se utiliza el “sistema de notación Miller”. Los índices de Miller de un plano cristalino se definen como el reciproco de las fracciones de intersección (con fracciones simplificadas) que el plano presenta con los ejes cristalográficos x, y y z de las tres aristas no paralelas de la celda unitaria cubica. Las aristas del cubo de la celda unitaria representan longitudes unidad, y las intersecciones de los planos reticulares se miden con base en estas longitudes unidad.
Los Índices de Miller para planos se representan equivalentemente al sistema cartesiano:
( h, k, l) = 1/(X,Y,Z) respectivamente.
Para identificar los planos de importancia se procede de la siguiente manera:
- Identificar los puntos donde cruza al plano de coordenadas X,Y,Z o también (h,k,l)en función de los parámetros de red (si el plano pasa por el origen se debe trasladar el origen del sistema de coordenadas).
- Los Índices de Miller para los planos cristalinos son el inverso a los puntos de un plano cartesiano.
- Se calculan los recíprocos o inversos de los puntos o intersecciones.
- Se multiplican o dividen estos números por un factor común.
- Si el reciproco es N/∞, donde N es cualquier numero entero real, esto significará en el plano que para este eje el plano quedará paralelo a él sin tocarlo.
- La cantidad obtenida siempre es menor a la unidad, caso que no ocurre en el estudio de las direcciones de los Índices de Miller. [1]
Ejemplo 3.9:
Determine los índices de Miller de los planos A, B y C (h,k,l)
Solución
Plano A
- x=1 y=1 z=1
- 1/x=1 , 1/y=1, 1/z=1
- No existen fracciones que eliminar
- (111)
Plano B
- Debe aclararse el plano no cruza al eje z, esto es debido al cociente entre 1/∞ lo cual con su respectivo limite tiende a ser cero (0)
- X=1 , y= 2, z=∞
- 1/x=1, 1/y=1/2, 1/z= 0
- Debemos eliminar las fracciones; 2(1, ½,0)
- (210)
- Es necesario cambiar el origen, ya que el plano pasa por el origen, ubicaremos el nuevo origen a la derecha del inicial, moviéndo en dirección del eje Y positivo
- Con el nuevo origen se tiene: x=∞, y=-1, z=∞
- 1/x=0, 1/y=-1, 1/z=0
- No existen fracciones que eliminar
Más ejemplos de planos:
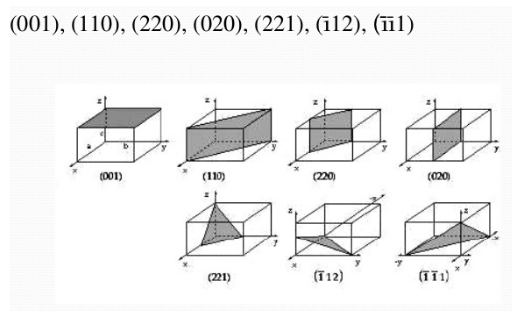 Figura 3.34 Ejemplos de planos.
Figura 3.34 Ejemplos de planos.
3.3.6. Familias de planos.
Se denomina familia de planos a el conjunto de planos formado por la combinación de los índices de Miller en un plano particular, en otras palabras se obtiene una familia de planos cuando se realizan todas las combinaciones posibles de los índices (h k l) incluyendo los índices negativos.
Aspectos importantes para los planos en los Índices de Miller:
- Los planos positivos y negativos son idénticos.
- Los planos y sus múltiplos no son idénticos. Esto se demuestra por medio de la densidad planar y el factor de empaquetamiento.
- Los planos de forma o familia de planos son equivalentes. Se representan con llaves {}
- En los sistemas cúbicos, una dirección es perpendicular a un plano si tiene los mismos Índices de Miller que dicho plano.
Ejemplo 3.10:
Familia de planos {110} en los sistemas cúbicos
 Figura 3.35 Familia de planos {110} en los sistemas cúbicos
Figura 3.35 Familia de planos {110} en los sistemas cúbicos
Estos planos son inversos en muchos aspectos de estudio, análisis y construcción.
Distancia entre planos cristalográficos en celdas unitarias cubicas
Una relación importante en el sistema cubico y solamente en el sistema cúbico, es que los índices de dirección de una dirección perpendicular a un plano cristalino tienen los mismos índices de Miller que el plano. Por ejemplo, la dirección [100] es perpendicular al plano cristalino (100).
El espacio interplanar entre dos planos paralelos con los mismos índices de Miller se define por medio de la siguiente gráfica:
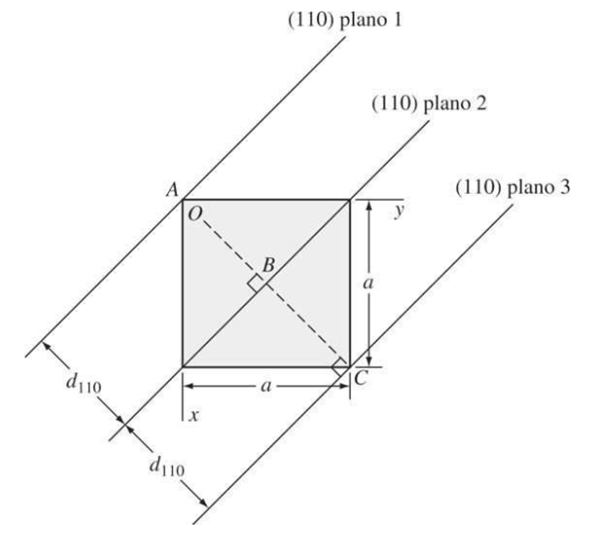 Figura 3.36 Vista superior de una celda cúbica mostrando la distancia entre cristalinos (110), d110. “Ciencia e ingeniería de materiales, Smith”.
Figura 3.36 Vista superior de una celda cúbica mostrando la distancia entre cristalinos (110), d110. “Ciencia e ingeniería de materiales, Smith”.
La distancia entre planos paralelos se define con la ecuación:
Donde dhkl: Espaciado interplanar entre planos paralelos contiguos con índices de Miller h, k y l.
a: constante de red (arista del cubo unidad).
h, k, l: índices de Miller de los planos cúbicos considerados.
3.3.7. Índices de Miller para celdas hexagonales
Para este tipo de estructura se ha desarrollado un especial conjunto de índices de Miller-Bravais, debido a la simetría de la estructura. En este se usan ya cuatro ejes, aunque es de tenerse en cuenta que el eje a3 es redundante.
El procedimiento para la obtención de planos y direcciones es el ya estudiado, aunque para el cálculo de las direcciones existen los métodos para tres ejes o el de cuatro ejes, siendo este último algo más tedioso.
En esta nueva estructura se tomaran los índices (h, k, i, l), para los cuales se asignara un eje respectivo (a1=h, a2=k, a3=i, c=l), teniendo en cuenta que para el eje a3 su existencia radicara en la relación h + k = -i; y la descomposición en cuatro vectores (creación de direcciones en cuatro ejes a partir de los índices en los tres ejes)
Relaciones:
H= 1/3(2h – k)
K=1/3(2k – h)
I=-1/3(h + k)
L=l
Ejemplo 3.11:
Determine los índices de Miller-Bravais para los planos A y B y par las direcciones C y D.
Solución
Plano A
- a1=a2=a3=∞, c=1
- 1/a1=1/a2=1/a3=0, 1/c=1
- No existen fracciones que simplificar
- (0001)
Plano B
Dirección C
- Dos puntos: 0,0,1 y 1,0,0
- Realizando la resta y tomando al punto 0,0,1 como cabeza del vector, se tiene: 0,0,1 – 1,0,0 = -1,0,1
- No existen fracciones que eliminar o enteros que reducir
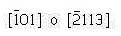
Dirección D
- Los puntos son: 0,1,0 y 1,0,0
- La resta genera el vector: 0,1,0 – 1,0,0 = -1,1,0
- No existen fracciones que eliminar ni enteros que reducir
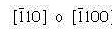
Comportamiento isotrópico y anisotrópico:
A causa de los arreglos en los diferentes planos y direcciones cristalográficas los materiales presentan comportamientos y desempeños diversos en sus propiedades mecánicas. Se dice que un material es cristalográficamente anisotrópico si sus propiedades dependen de la dirección cristalográfica en la cual se mide la propiedad. Si sus propiedades son idénticas en cualquier dirección el material se conoce cristalográficamente como isotrópico. Puede suceder que un material pase de ser anisotrópico a isotrópico si sus arreglos son aleatorios en forma policristalina. En genera los materiales policristalino as muestran propiedades isotrópicas. Ejemplo de ello tenernos el aluminio, el cual si posee idénticas propiedades en todas las direcciones diremos que es un elemento cristalográficamente isotrópico, pero si se presenta en forma policristalina se puede asumir o comportar como anisotrópico.[2]
REFERENCIAS.
- Askeland, Donald R; Phule, Pracleep; Ciencia e Ingeniería de los Materiales; International Thomson Editores, cuarta edición, México, 2004.
- Smith, William F (Autor); Hashemi, Javad ( Colaborador); Cruells Cadevall, Montesrrat ( Revisor); Roca Vallmajor, Antoni ( Revisor); España, Mcgraw- Hill Interamericana S.A, 2004.
3.3.8. Planos Cristalinos:
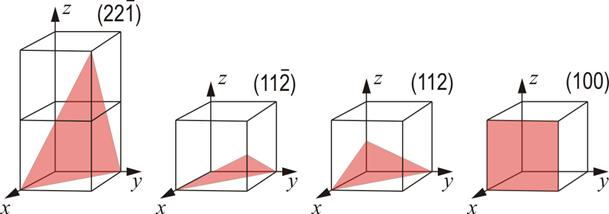 Figura 3.38 “Planos cristalinos”.
Figura 3.38 “Planos cristalinos”.
Dirección en la celda
A menudo, es necesario referirnos a posiciones específicas en las redes cristalinas. Esto es especialmente importante para metales y aleaciones con propiedades que varían con la orientación cristalográfica. Para cristales cúbicos los índices de las direcciones cristalográficas son los componentes vectoriales de las direcciones resueltos a lo largo de cada eje coordenado y reducido a los enteros más pequeños.
Para indicar en un diagrama la dirección en una celda cúbica unitaria dibujamos un vector de dirección desde el origen (que es normalmente una esquina de la celda cúbica) hasta que sale la superficie del cubo. Las coordenadas de posición de la celda unidad donde el vector de posición sale de la superficie del cubo después de ser convertidas a enteros son los índices de dirección. Los índices de dirección se encierran entre corchetes sin separación por comas.
Planos en una celda unitaria
Las superficies cristalinas en celdillas unidad HCP pueden ser identificadas comúnmente utilizando cuatro índices en lugar de tres. Los índices para los planos cristalinos HCP, llamados índices Miller-Bravais, son designados por las letras h, k, i, l y encerrados entre paréntesis ( hkil ). Estos índices hexagonales de 4indices están basados en un sistema coordenado de 4 ejes.
Existen 3 ejes básicos, a1, a2, a3, que forman 1200 entre sí. El cuarto eje o eje c es el eje vertical y está localizado en el centro de la celdilla unidad. La unidad a de medida a lo largo de los ejes a1 a2 a3 es la distancia entre los átomos a lo largo de estos ejes. La unidad de medida a lo largo del eje es la altura de la celdilla unidad. Los recíprocos de las intersecciones que un plano cristalino determina con los ejes, a1, a2, a3 proporciona los índices h, k e i mientras el recíproco de la intersección con el eje c da el índice l.
Notación para planos
Los planos basales de la celdilla unidad HCP son muy importantes para esta celdilla unidad puesto que el plano basal de la celdilla HCP es paralelo a los ejes, a1, a2, a3 las intersecciones de este plano con estos ejes serán todas de valor infinito. Así, a1 =”, a2 =”, a3 =” El eje c, sin embargo, es único puesto que el plano basal superior intercepta el eje c a una distancia unidad. Tomando los recíprocos de estas intersecciones tenemos los índices de Miller-Bravais para el plano Basal HCP. Así, H =0 K=0 I = 0 y L=1. El plano basal es, por tanto un plano cero-cero-cero-uno o plano (0001).
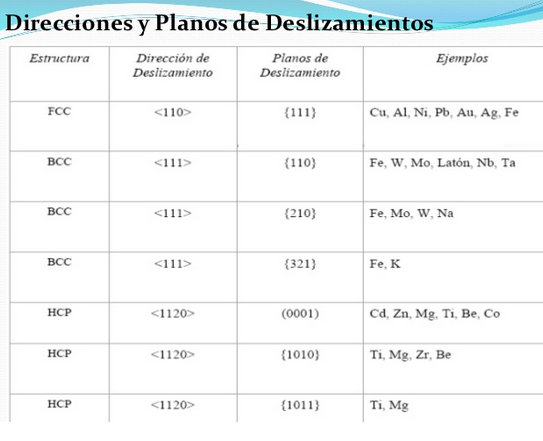 Figura 3.39 Direcciones de planos y desplazamientos para estructuras cristalinas.
Figura 3.39 Direcciones de planos y desplazamientos para estructuras cristalinas.
3.3.9. Densidad Planar:
Relación entre el número de átomos completos contenidos en un plano y el área del plano
Es una parte de la anisotropía, que se dedica al estudio de los procesos de deformación de los materiales, pues estos se producen donde la densidad linear o planar es alta, y se deforma por el deslizamiento de los átomos en esa dirección. Se calcula porque los átomos no forman esferas perfectas, tienen imperfecciones, que son las que se estudian con este tipo de investigaciones.
Pero una definición más formal la densidad planar es el número de átomos que tienen sus centros localizados dentro de un área dada sobre un plano. El área planar seleccionada debe ser representativa de los grupos de átomos repetitivos dentro del plano. Cuando ocurre deslizamiento bajo esfuerzo (deformación plástica), éste ocurre en los planos sobre los cuales los átomos están más densamente empacados.
La densidad planar en cristalografía nos muestra que tan lleno de átomos esta un plano lo cual es muy importante porque podemos conocer cómo se van a deslizar estos planos unos con respecto a otros; con su respectiva dirección de deslizamiento ( densidad lineal) ; la combinación de estos dos densidad planar y lineal me dan a conocer la deformación del material, A la combinación de un plano de deslizamiento con una dirección, es a lo que se le denomina sistema de deslizamiento, y es a través de estos sistemas por donde se produce la deformación de los materiales, de tal forma que cuanto mayor es el número de ellos mayor será la capacidad de deformación de éstos. Para poder determinar cuáles son sistemas existentes, primero tenemos que ver cuáles son los planos y direcciones preferentes. Pues bien los planos de deslizamiento son los que poseen la fracción atómica planar (FAP) más grande o lo que es lo mismo, son los planos de mayor compacidad en la estructura cristalina.
Ejemplo 3.12:
Calcule la densidad atómica planar ρp en el plano (110) de la red BCC del hierro a en átomos por milímetro cuadrado. La constante de red del hierro a es 0.287 nm.
Solución
Ejemplo 3.13:
Densidad planar de familias 100, 110 y 111. Protección descriptiva de planos y corte de átomos.
Inicialmente podemos definir la densidad planar, coma la cantidad de átomos que hay en un determinado plano ejemplo: familia de planos (100). Pero una definición más formal la densidad planar es el número de átomos que tienen sus centros localizados dentro de un área dada sobre un plano. El área planar seleccionada debe ser representativa de los grupos de átomos repetitivos dentro del plano. Cuando ocurre deslizamiento bajo esfuerzo (deformación plástica), éste ocurre en los planos sobre los cuales los átomos están más densamente empacados.
La densidad planar en cristalografía nos muestra que tan lleno de átomos esta un plano lo cual es muy importante porque podemos conocer cómo se van a deslizar estos planos unos con respecto a otros; con su respectiva dirección de deslizamiento ( densidad lineal) ; la combinación de estos dos densidad planar y lineal me dan a conocer la deformación del material, A la combinación de un plano de deslizamiento con una dirección, es a lo que se le denomina sistema de deslizamiento, y es a través de estos sistemas por donde se produce la deformación de los materiales, de tal forma que cuanto mayor es el número de ellos mayor será la capacidad de deformación de éstos. Para poder determinar cuáles son sistemas existentes, primero tenemos que ver cuáles son los planos y direcciones preferentes. Pues bien los planos de deslizamiento son los que poseen la fracción atómica planar (FAP) más grande o lo que es lo mismo, son los planos de mayor compacidad en la estructura cristalina. Se define la fracción (1) atómica planar como:
- ∂= #átomos intersectados/área del plano.
Redes cristalinas BCC Y FCC.
Estructura cúbica centrada en cuerpo (BCC)
Esta estructura recibe la designación de I y en ella todos los ejes son iguales a = b = c y sus ángulos son de 90º. El parámetro reticular es a. Sí se coloca un átomo en cada punto de la red de Bravais cúbica centrada en cuerpo, tengo 8 átomos en los vértices y uno en el interior.
Figura 3.40 Estructura cúbica BCC
El átomo central toca a todos los átomos de los vértices a través de ladiagonal del cubo. Éste n° de átomos que tocan al átomo central son los vecinos inmediatos y es lo que se denomina nº de coordinación. Luego en esta estructura NC = 8.
Estructura cúbica centrada en caras FCC:
Se designa con la letra FCC. Todos los ejes unitarios son iguales y sus ángulos son de 90º, siendo el parámetro reticular a. Si colocamos un átomo en cada punto de la red de Bravais cúbica centrada en caras, tendremos 6 átomos en los seis centros de caras, además de los 8 de los vértices.
Figura 3.41 Estructura cúbica FCC.
Cálculo de la densidad planar.
Para calcular la densidad planar usamos la siguiente convención. Si un átomo pertenece totalmente a un área dada, tal como la del átomo localizado en el centro de una cara en una estructura FCC, notamos que la huella de la intersección del átomo sobre el plano es un círculo. Entonces, dentro del área contamos un átomo en el centro y un cuarto de átomo en cada una de las esquinas, ya que cada uno intercepta solamente un cuarto de círculo en el área. La densidad planar o del plano es 2/a2. Debemos agregar que en estos cálculos de la densidad, una de las reglas básicas es que un plano o una línea debe pasar a través del centro de un átomo no se cuenta el átomo en los cálculos.
Si determinamos la densidad planar de las distintas familias de planos de las diferentes estructuras, veremos que para el caso de la FCC, la familia de planos de mayor densidad planar es la {111}, mientras que para la estructura BCC, es la {110}.Luego los planos pertenecientes a estas familias constituyen los planos de deslizamientos de sus estructuras cristalinas correspondientes. Por lo que ya solo necesitamos conocer, Para poder determinar los sistemas, cuales son las direcciones de deslizamientos.
A continuación veremos el cálculo de la densidad atómica planar de la familia de planos (100), (110), (111):
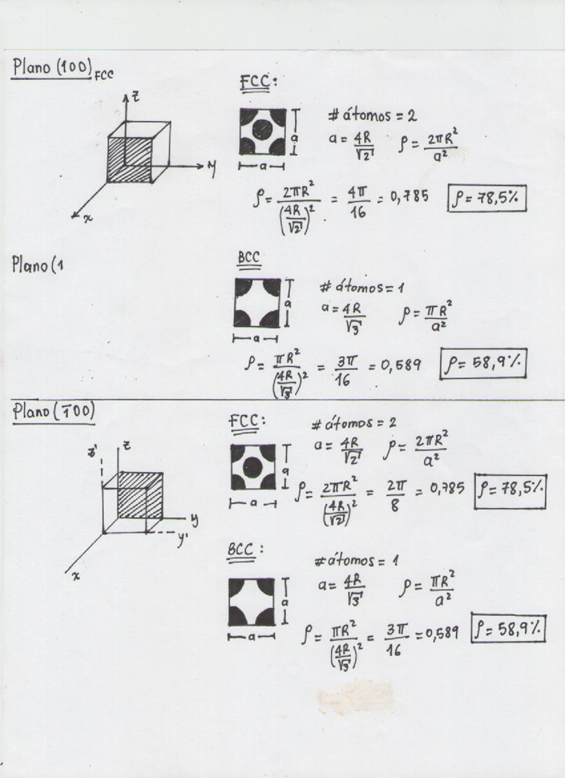 Figura 3.42. Explicación de cálculo de densidad planar de las estructuras cristalinas FCC y BCC en dos planos de la misma familia.
Figura 3.42. Explicación de cálculo de densidad planar de las estructuras cristalinas FCC y BCC en dos planos de la misma familia.
Con los resultados anteriores, y después de hallar la densidad planar para diferentes planos de la familia (100) se llega a la conclusión que para FCC es igual a 78,5% y para BCC es igual a 58,9%.
Como ya quedó dicho en la introducción, para calcular la densidad planar, el área del plano debe pasar por el centro del átomo, para poder tener en cuenta a éste como un átomo representativo, por eso, para calcular la densidad planar en una red cristalina BCC debemos garantizar que el plano no intercepte el átomo central. Aquello es posible saberlo haciendo proyección del área y del plano, utilizando geometría analítica.
Para el plano (111) BCC se ha hecho con anterioridad una proyección y se ha deducido que el átomo central no corta lo suficiente al área del plano como para tomarse como un átomo representativo, después de esto se pasa a hacer un cálculo de la densidad planar, sin tenerlo en cuenta. A continuación se mostrará el desarrollo de lo anteriormente mencionado:
 Figura 3.43 Explicación de cálculo de densidad planar de las estructuras cristalinas FCC y BCC.
Figura 3.43 Explicación de cálculo de densidad planar de las estructuras cristalinas FCC y BCC.
Con los resultados anteriores, y después de hallar la densidad planar para diferentes planos de la familia (111) se llega a la conclusión que para FCC es igual a 90,7% y para BCC es igual a 34%.
 Figura 3.44 Explicación de cálculo de densidad planar de las estructuras cristalinas FCC y BCC.
Figura 3.44 Explicación de cálculo de densidad planar de las estructuras cristalinas FCC y BCC.
Con los resultados anteriores, y después de hallar la densidad planar para diferentes planos de la familia (110) se llega a la conclusión que para FCC es igual a 55,53% y para BCC es igual a 83,3%.
REFERENCIAS
- http://www.uhu.es/beatriz.aranda/apuntesciemat/TEMA%201funcmat.pdf
- SMITH, F. WILLIAM, Fundamentos de la ciencia e ingeniería de materiales
3.4 DIFRACCIÓN DE RAYOS X
Objetivos:
- Comprender la aplicación de la difracción de rayos x en la cristalografía.
- Deducir la fórmula que relaciona la longitud de onda (λ), la distancia entre planos cristalinos (d), el parámetro de red (a) y el ángulo de incidencia de los rayos x (θ).
- Conocer algunos métodos de difracción de rayos x.
- Conocer algunos equipos que intervienen en el uso de rayos x para el estudio de la cristalografía.
- Resolver algunos ejemplos sobre la aplicación de difracción de rayos x en la cristalografía.
3.4.1 Introducción
Los Rayos X se descubrieron en 1895 por el físico alemán Röntgen y recibieron ese nombre porque se desconocía su naturaleza en ese momento. A diferencia de la luz ordinaria, esa radiación era invisible pero viajaba en línea recta y ennegrecía las películas fotográficas de manera similar a como lo hacía la luz. Sin embargo, esa radiación era mucho más penetrante que la luz y podía atravesar el cuerpo humano, la madera, piezas delgadas de metal, etc. Esta propiedad encontró inmediatamente aplicación en la obtención de radiografías: las porciones menos densas de un material dejan pasar la radiación X en mayor proporción que las más densas: de esta forma es posible localizar la posición de una fractura en un hueso o una grieta en una pieza metálica. En 1912 se estableció de manera precisa la naturaleza de los rayos X. En ese año se descubrió la difracción de rayos x en cristales y este descubrimiento probó la naturaleza de los rayos X y proporcionó un nuevo método para investigar la estructura de la materia de manera simultánea. Los R-X son radiación electromagnética de la misma naturaleza que la luz pero de longitud de onda mucho más corta. La unidad de medida en la región de los r-x es el angstrom (Å), igual a 10-10 m y los rayos x usados en difracción tienen longitudes de onda en el rango 0.5-2.5 Å mientras que la longitud de onda de la luz visible está en el orden de 6000 Å. De acuerdo con la teoría cuántica, la radiación electromagnética puede considerarse tanto un movimiento ondulatorio como un haz de partículas llamadas fotones. Cada fotón lleva asociada una energía hn, donde h es la cte de Planck (6.63×10-34 J·s); se establece así un vínculo entre las dos teoría ya que la frecuencia del movimiento ondulatorio puede calcularse a partir de la energía del fotón y viceversa.
3.4.2 Cristalografía de rayos X
La cristalografía de rayos x es una técnica que consiste en hacer pasar un haz de luz a través de un cristal de la sustancia o el material en estudio. El haz se dispersa en varias direcciones debido al orden de los átomos en el cristal y, por difracción, se puede observar un patrón de intensidades que se interpreta según la ubicación de los átomos, haciendo uso de la LEY DE BRAGG.
Una de las limitaciones de esta técnica es que solo se puede usar en materiales cristalinos, por lo tanto, no puede ser usada en sustancias como gases, disoluciones, a sistemas amorfos, entre otros.
Ley de Bragg
Para interpretar los diagramas de difracción se requiere una teoría. W. Bragg fue pionero en el tema y desarrolló una sencilla teoría, que es la que veremos. En este modelo se analiza la interacción de un haz de radiación sobre un conjunto de planos paralelos, equiespaciados y semitransparentes a la radiación. Para efectos de la reflexión se aplica que el ángulo de incidencia es igual al de reflexión.
La interferencia es constructiva cuando la diferencia de fase entre la radiación emitida por diferentes átomos es proporcional a 2π. Esta condición se expresa en la ley de Bragg:
Ecuación 3.5.
Donde:
- n es un número entero.
- λ es la longitud de onda de los rayos X.
- des la distancia entre los planos de la red cristalina y.
- θ es el ángulo entre los rayos incidentes y los planos de dispersión.
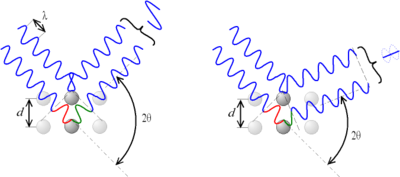 Figura 3.45 Incidencia de rayos x sobre dos planos.
Figura 3.45 Incidencia de rayos x sobre dos planos.
De acuerdo al ángulo de desviación (2θ), el cambio de fase de las ondas produce interferencia constructiva (figura izquierda) o destructiva (figura derecha).
La esfera de Ewald:
Para visualizar fácilmente los planos de Miller que contribuyen a la difracción en una dirección dada y determinar la relación entre la orientación del cristal y el patrón de difracción, se utiliza la construcción conocida como esfera de Ewald. La esfera de Ewald ilustra todas las posibles direcciones en que los rayos X pueden ser reflejados por el cristal. El radio de esta esfera es y su extremo en la dirección del haz de rayos X incidente coincide con el origen de la red recíproca.
Si un punto de la red recíproca de coordenadas se encuentra sobre la superficie de la esfera de Ewald, los planos de Miller con índices darán lugar a un punto de difracción en la dirección definida por el centro de la esfera y ese punto de la red recíproca. La distancia entre el origen y, por lo que se puede demostrar geométricamente que esta condición de difracción es equivalente a la ley de Bragg.
Acerca de la distancia interplanar (d) y el parámetro de red (a):
En las estructuras cristalinas cúbicas, el espaciado interplanar entre dos planos paralelos con los paralelos con los mismos índices de Miller se indica como dhkl, donde h, k y l son los índices de Miller de los planos. Este espaciado representa la distancia desde un origen elegido que contiene a un plano a otro paralelo con los mismos índices que sea cercano al primero.
Por simple geometría, se puede demostrar que para las estructuras cristalinas cúbicas:
Ecuacion 3.6.
Donde:
dhkl= espaciado interplanar entre planos paralelos contiguos con índices de Miller h, k y l.
a = constante de red (arista del cubo unidad).
h, k, l = índices de Miller de los planos cúbicos considerados.
3.4.3 Algunas aplicaciones de la difracción de rayos x.
3.4.3.1 Identificacion de fases:
Una fase cristalina dada siempre produce un patrón de difracción característico, bien esté en estado puro o como constituyente de una mezcla. Este hecho es la base para el uso de la difracción como método de análisis químico. El análisis cualitativo se realiza mediante la identificación del patrón de esa fase. Para la identificación cualitativa se usa la Powder Diffraction File, esta base de datos contiene datos de d-I además de información cristalográfica y bibliográfica para gran cantidad de fases crist. de materiales inorgánicos, minerales, productos farmacéuticos, etc
Figura 3.47. Power Diffraction File
3.4.3.2 Determinación de estructuras cristalinas:
El proceso de determinación de una estructura mediante drx comienza con la toma de datos con suficiente precisión en un intervalo amplio de 2θ. La siguiente etapa es el indexado, los programas más habituales para llevar a cabo el indexado son ITO, TREOR y DICVOL entre otros. La siguiente etapa, ajuste de perfil, permite asignar intensidades, forma y anchura de picos, background; existen dos técnicas diferentes: el método de Le Bail y el método de Pawley.
Una vez obtenidas las intensidades de las reflexiones es necesario obtener una aproximación inicial de la estructura, para ello se pueden emplear métodos tradicionales como los de Patterson o directos así como métodos basados en el espacio directo. Por último se realiza el refinamiento de la estructura utilizando el método de Rietveld en el que se minimiza la diferencia entre la intensidad calculada y la medida experimentalmente.
3.4.3.3 Estudio de texturas:
Cada grano en un agregado policristalino normalmente tiene una orientación cristalográfica diferente de la de sus vecinos. Considerado como un todo las orientaciones de todos los granos pueden estar aleatoriamente distribuidas o pueden tender a agruparse, en mayor o menor grado alrededor de una o varias orientaciones particulares. Cualquier agregado caracterizado por esta condición se dice que posee orientación preferente o textura. La orientación preferente puede tener una gran influencia sobre las intensidades de los picos de difracción.
La orientación preferente es un fenómeno muy frecuente, en metales, materiales cerámicos, películas semiconductoras y recubrimientos en general entre otros. De hecho, la presencia de orientación preferente es la regla habitual, no la excepción. Las texturas más frecuentes son en forma de fibras o en forma de láminas. En la textura fibrosa en la mayoría de los granos la misma dirección cristalográfica [uvw] es paralela o casi paralela al eje del alambre. En el caso de la textura en láminas la mayoría de los granos están orientados con cierto plano cristalográfico (hkl) aproximadamente paralelo a la superficie de la lámina y una dirección en ese plano [uvw] aproximadamente paralela a la dirección en la que se aplanó la lámina.
La mayoría de las texturas laminares, sin embargo, sólo pueden describirse mediante la suma de un número de orientaciones ideales o componentes de textura; esto sólo puede hacerse mediante una descripción gráfica tal como la figura de polo.
El uso de las figuras de polo para representar texturas puede ilustrarse mediante el siguiente ejemplo: supongamos una lámina de un metal cúbico que contiene sólo 10 granos y la orientación de esos granos es conocida. Las orientaciones de esos 10 granos puede resumirse representando las posiciones de los polos {100} en una única proyección estereográfica con el plano de proyección paralelo a la superficie de la lámina. Puesto que cada grano posee tres polos {100} habrá un total de 30 polos representados en la proyección. Si los granos tienen una orientación completamente aleatoria esos polos aparecerán uniformemente distribuidos sobre la proyección. Sin embargo, si existe orientación preferente los polos tenderán a agruparse en ciertas areas de la proyección dejando otras vacías.
Figura 3.48. Figuras de polo.
Para determinar experimentalmente la textura de un material se fija la posición de tubo y detector (2θ) para estudiar una reflexión (hkl) determinada. [6]
3.4.4 Algunos métodos de análisis por difracción de rayos x.
Existen tres métodos para producir difracción de rayos X.
- Método de Powder
- método Laue
- método de rotación de cristal.
3.4.4.1 Método de análisis de polvo por difracción de rayos x:
La técnica comúnmente utilizada en difracción de rayos x es el método de polvo. En ésta técnica se utiliza una muestra pulverizada de muchos cristales para que tenga lugar una orientación al azar y asegurar que algunas partículas estarán orientadas en el haz de rayos x para que cumplan las condiciones de difracción de la ley de Bragg.
Los datos de los análisis de rayos x por difracción de las celdas unitarias pueden simplificarse expresando la longitud de onda así:
Ecuación 3.7.
Empleando la anterior ecuación junto con los datos de difracción de rayos x podemos determinar si una estructura es cúbica centrada en el cuerpo (BCC) o cúbica centrada en las caras (FCC). Para esto debe conocerse cuáles planos cristalinos son planos de difracción para cada tipo de estructura cristalina:
- Para la red cúbica sencilla, todos los planos (hkl) son planos de reflexión.
- Para la estructura BCC la difracción solo se da en los planos cuyos índices de Miller sumados (h+k+l) dan un número par.
- En la estructura FCC los principales planos de difracción son los que sus índices son todos pares o todos impares (el cero se considera par).
Reglas para determinar los planos de difracción {hkl} en los cristales cúbicos:
Tabla 3.46 Reglas para planos de difracción en cristales cúbicos.
Índices de Miller de los planos de difracción para las redes BCC y FCC:
Tabla 3.47 Índices de Miller de los planos de difracción para las redes BCC y FCC.
Un caso sencillo que permite ilustrar cómo se puede emplear este análisis es diferenciar entre las estructuras cristalinas BCC y FCC de un metal cúbico. Supóngase que se tiene un metal con una estructura cristalina BCC o FCC y que se pueden identificar los planos de difracción principales y los valores de 2θ correspondientes.
Despejando y elevando al cuadrado ambos lados se tiene:
Ecuación 3.8.
A partir de los resultados experimentales de difracción de rayos x se pueden obtener los valores de 2θ para una serie de planos principales de difracción {hkl}. Como y se pueden eliminar estos valores con la relación de dos valores de sin2θ.
θA y θB: son los dos ángulos de difracción asociados a los planos principales escogidos.
Para la estructura cristalina BCC los dos primeros planos principales son {1 1 0} y {2 0 0}. Sustituyendo h, k y l en la ecuación anterior se tiene:
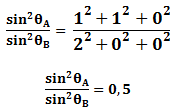 Del resultado anterior podemos concluir que un metal es BCC si la relación de de los planos primeros planos principales de difracción es 0,5.
Del resultado anterior podemos concluir que un metal es BCC si la relación de de los planos primeros planos principales de difracción es 0,5.
Para la estructura cristalina FCC los dos primeros planos principales son {1 1 1} y {2 0 0}. Sustituyendo h, k y l en la ecuación anterior se tiene:
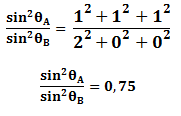 Del resultado anterior podemos concluir que un metal es FCC si la relación de de los planos primeros planos principales de difracción es 0,75.
Del resultado anterior podemos concluir que un metal es FCC si la relación de de los planos primeros planos principales de difracción es 0,75.
3.4.4.2 Método de laue:
Consiste en hacer incidir en un cristal un espectro continuo de rayos X, de tal manera que para cada longitud de onda, existirá un determinado ángulo. El método de transmisión de Laue (a) en la figura consiste en colocar esta película detrás del cristal como se ve a la derecha. Por el contrario, en el método de reflexión (b) en la figura de Laue, la película se interpone entre la fuente y el cristal, esta posee un agujero que deja pasar los haces de rayos X.
En el método de transmisión de Laue los haces difractados forman un patrón de machas circular o elíptico y en cambio, el patrón formado en el método de reflexión de Laue son hipérbolas.
 Figura 3.49 Diagrama de Laue de un cristal.
Figura 3.49 Diagrama de Laue de un cristal.
3.4.4.3 Método de rotación de cristal:
Se hace incidir un haz de rayos X monocromáticos sobre un cristal. Para detectar los haces difractados, la película es envuelta de forma cilíndrica de tal manera que rodee al cristal. El cristal se hace girar sobre el eje perpendicular al haz incidente, el cual coincide con el eje del cilindro. Para encontrar el ángulo al cual se cumple la ley de Bragg, el giro del cristal se hace sucesivamente de 0° a 90°, hasta encontrar el patrón de difracción mostrado en la figura.
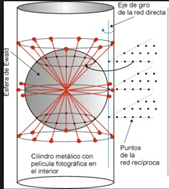 Figura 3.50 Esquema del método de rotación de cristal.
Figura 3.50 Esquema del método de rotación de cristal.
EL DIFRACTÓMETRO
El difractómetro de rayos X es capaz de detectar la radiación que emana una muestra determinada al ser excitada por una fuente de energía. La respuesta generada depende del ordenamiento interno de sus átomos. El difractómetro está compuesto de un portamuestras móvil que irá moviendo el objeto estudiado con el fin de variar el ángulo de incidencia de los rayos X. De este modo la estructura atómica de la muestra quedará registrada en un difractógrama. [5]
Figura 3.51 Difractómetro.
Ejemplo 3.14:
Una muestra de hierro BCC se coloca en un difractómetro de rayos X utilizando rayos X incidentes de longitud de onda λ = 0,1541 nm. La difracción a partir de los planos {1 1 0} se obtiene a 2θ = 44,704 º. Calcule el valor de la constante de red a para el hierro BCC, suponga un orden de difracción de n = 1.
Solución
Ejemplo 3.15:
El difractograma de un elemento que tiene estructura cúbica BCC o FCC presenta picos de difracción en los ángulos 2θ siguientes: 40, 58, 73, 86.8, 100.4 y 114.7. La longitud de onda de los rayos X incidentes utilizados es de 0. 154 nm.
- Determine la estructura cúbica del elemento.
- Determine la constante de red del elemento.
- Identifique al elemento.
Solución:
a. Determinación de la estructura cristalina del elemento.
Primero se calculan los valores de sin2θ a partir de los valores de 2θ de los ángulos de difracción.
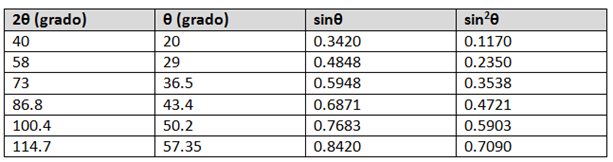 A continuación se calcula la relación entre los valores de sin2θ de los ángulos primero y segundo:
A continuación se calcula la relación entre los valores de sin2θ de los ángulos primero y segundo:
![]() La estructura cristalina es BCC ya que la relación es de ≈ 0.5. Si la relación hubiera sido ≈ 0.75, la estructura seria FCC.
La estructura cristalina es BCC ya que la relación es de ≈ 0.5. Si la relación hubiera sido ≈ 0.75, la estructura seria FCC.
b. Determinación de la constante de red.
Sustituyendo h = 1, k = 1 y l = 0 en la ecuación anterior para los índices de Miller h, k y l de la primera serie de planos principales de difracción para la estructura BCC, que son planos {1 1 0}, el valor correspondiente a sin2θ es 0.117, y para una radiación incidente de λ, 0.154 nm, se obtiene:
c. Identificación del elemento.El elemento es el volframio, dado que el elemento tiene una constante de red de 0.316 nm y es BCC.
EJERCICIOS PROPUESTOS
1. Una muestra de metal BCC se coloca en un difractómetro de rayos X utilizando rayos X de longitud λ = 0.1541 nm. La difracción de los planos {2 2 1} se obtiene a 2θ = 88.838º. Calcule un valor para la constante de red para este metal BCC. (Suponga una difracción de primer orden, n = 1).
2. Rayos X de longitud de onda desconocida se difractan por una muestra de oro. El ángulo 2θ es de 64.582º para los planos {2 2 0}. ¿Cuál es la longitud de onda de los rayos X utilizados? (La constante de celda del oro es = 0.40788 nm; suponga una difracción de primer orden, n = 1).
3. Un difractograma para un elemento que tiene una estructura cristalina BCC o FCC presenta picos de difracción a los valores de ángulo 2θ siguientes: 41.069 º, 47.782º, 69.879º y 84.396º. (La longitud de onda de la radiación incidente es de 0.15405 nm).
a. Determine la estructura cristalina del elemento.
b. Determine la constante de red del elemento.
c. Identifique el elemento.
4. Un difractograma para un elemento que tiene una estructura cristalina BCC o FCC presenta picos de difracción a los valores de ángulo 2θ siguientes: 38.68º, 55.71º, 69.70º, 82.55º, 95.00º y 107.67º. (La longitud de onda de la radiación incidente es de 0.15405 nm).
a. Determine la estructura cristalina del elemento.
b.Determine la constante de red del elemento.
c.Identifique el elemento.
REFERENCIAS
- D. Cullity S.R. Stock “Elements of X-Ray Diffraction” 3rd Ed. Prentice Hall 2001
- Hammond “The Basics of Crystallography and Diffraction” International Union of Crystallography, Oxford University Press, 2000
- Giacovazzo, editor “Fundamentals of Crystallography” International Union of Crystallography, Oxford University Press, 1998
- Glatter and O. Kratky “Small Angle X-ray Scattering” New York: Academic Press, 1982.
- Difractometro de rayos x; recuperado el 11/05/15 de http://malagainnova.wordpress.com/2008/09/03/el-difractometro-de-rayos-x-de-la-uma-permite-conocer-el-ordenamiento-interno-de-los-materiales/
- http://www.upct.es/~minaeees/difraccion_rayosx.pdf
3.5. IMPERFECCIONES CRISTALINAS.
En el arreglo de los átomos o iones de los materiales diseñados existen imperfecciones o defectos. Con frecuencia, estos defectos tienen un impacto directo sobre las propiedades mecánicas y físicas de los materiales. Estas, afectan de cierta manera algunas propiedades de materiales que son relevantes en ingeniería, como por ejemplo, la conductividad eléctrica en algunos semiconductores, la corrosión de los metales, y la capacidad de formarse aleaciones en frio, etc. En esta parte hablaremos de:
- Defectos puntuales.
- Defectos de línea (dislocaciones).
- Defectos superficiales y límites de grano internos.
- Defectos tridimensionales macroscópicos.(volumétricos).
3.5.1. Imperfecciones o defectos puntuales:
Un defecto puntual implica en general a uno o un par de átomos o iones y, en consecuencia es distinto de los defectos extendidos, como dislocaciones, límites de grano, etc. Un “punto” importante acerca de los defectos es que, aunque se presentan en uno o dos sitios, su presencia es en distancias mucho mayores en el material cristalino. Son de 3 tipos:
- Átomos intersticiales.
- Vacancias.
- Átomos sustitucionales.
3.5.1.1. Átomos intersticiales:
Se forman cuando se inserta un átomo o ion adicional en la estructura cristalina en una posición normalmente desocupada, este defecto no ocurre de manera natural debido a la distorsión estructural que se genera, pero se puede realizar por medio de irradiación.
Los átomos o los iones intersticiales, aunque son mucho menores que los átomos o los iones que están en los puntos de red, son mayores que los sitios intersticiales que ocupan; en consecuencia, la región cristalina vecina esta comprimida y distorsionada.
Los átomos intersticiales como los de hidrogeno están presentes, con frecuencia, como impurezas, mientras que los átomos de carbono se agregan en forma intersticial al hierro para producir acero. Para concentraciones pequeñas, los átomos de carbono ocupan sitios intersticiales en la estructura cristalina del hierro e introducen un esfuerzo en la región del cristal en su cercanía.
Si hay dislocaciones en los cristales al tratar de mover esos tipos de defectos, se encuentran con resistencia a su movimiento, con lo que se vuelve difícil crear deformación permanente en metales y aleaciones. Esta es una forma importante de aumentar la resistencia de los materiales metálicos. A diferencia de las vacancias, una vez introducidos, la cantidad de átomos o iones intersticiales en la estructura permanece casi constante, aun cuando se cambie la temperatura.
 Figura 3.52 Átomos intersticiales. [2]
Figura 3.52 Átomos intersticiales. [2]
3.5.1.2. Vacancias:
constituye el defecto puntual más simple, además es un hueco creado por la pérdida de un átomo. Puede producirse durante la solidificación por perturbaciones locales durante el crecimiento de los cristales, también pueden deberse a los reordenamientos atómicos de estos cristales ya formados, como consecuencia de la movilidad de los átomos.
Las vacantes en los metales pueden ser generadas por:
- Deformación plástica del metal
- Enfriamiento rápido de mayores a menores temperaturas
- Por la acción energética de algunas partículas como los neutrones.
NOTA: Los clusters son los que están formadas por vacantes no equilibradas que tiene a agruparse entre sí.
3.5.1.3. Átomos sustitucionales:
En este defecto se sustituye un átomo de la estructura cristalina por otro, este átomo permanece en la posición original. Se debe tomar en cuenta que el radio del átomo no debe ser diferente de un 15% ya sea en mayor o menor proporción ya que podrían ocurrir perturbaciones en el material. Un átomo de mayor radio hará que los átomos vecinos sufran una compresión, y un átomo sustituido de menor radio hará que los átomos vecinos sufran una tensión.
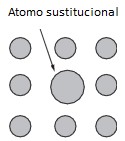 Figura 3.54 Átomo sustitucional.
Figura 3.54 Átomo sustitucional.
3.5.1.4. Defecto Frenkel:
Es una imperfección cristalina combinada de la vacancia y de la intersticial, ocurre cuando un ion salta de un punto normal dentro de la red a uno intersticial dejando entonces una vacancia. Es el conjunto formado por un átomo intersticial y el hueco que ha dejado tras el salto.
En el caso de un cristal iónico, los cationes son más pequeños que los aniones; son predominantes los defectos Frenkel de los cationes. Este tipo de defectos son los que confieren movilidad iónica al sólido. Ejemplo: el más simple y conocido el cloruro de sodio.
Este defecto es ilustrado con un ejemplo de cloruro de sodio; los diagramas son una representación en 2 dimensiones de lo que ocurre realmente en 3:
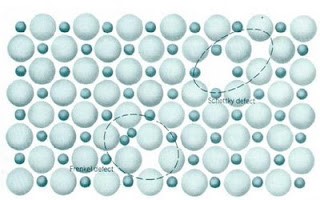 Figura 3.55. Defecto Frenkel. [4]
Figura 3.55. Defecto Frenkel. [4]
3.5.1.5. Defecto Schottky:
Es un par de vacancias en un material con enlaces iónicos. Para mantener la neutralidad deben perderse de la red tanto un catión como un anión.
El defecto es típico de los materiales cerámicos, pues es un defecto que aparece para mantener la electroneutralidad del material. Se generan vacantes de iones de signo contrario para anularse de forma estequiometria; con el fin de mantener una carga total neutra. Cada vacante es un defecto de Schottky por separado.
Es exclusivo de los materiales iónicos y suele encontrarse en muchos materiales cerámicos. En este defecto, las vacancias se presentan en un material con enlaces iónicos; donde debe faltar un número estequiométrico de aniones y cationes en el cristal si se quiere conservar en el la neutralidad eléctrica. Por ejemplo, un Mg+2 y un O-2 iones faltantes en Mg constituyen un par de Schottky. En el Zr+4 faltante, habrá 2 iones O-2 faltantes.
 Figura 3.56 Defecto Schottky. [5]
Figura 3.56 Defecto Schottky. [5]
3.5.2. Imperfecciones o defectos lineales:
Se dan en dirección de los planos de Miller; debido a la ausencia conjunta de átomos alineados en súplanos, la existencia de dislocaciones en los materiales metálicos justifica la plasticidad y fluencia que los caracterizan y diferencian frente a los cerámicos. Estos aun teniendo también estructura cristalina no permiten los procesos de plastificación.
Las dislocaciones son defectos de línea que se mueven al aplicar una fuerza al material haciendo que se deforme. El esfuerzo cortante resultante crítico es el esfuerzo requerido para que se mueva la dislocación. La dislocación se mueve en un sistema de deslizamiento, formado por un plano de deslizamiento y una dirección de deslizamiento. La dirección de deslizamiento, típicamente es una dirección compacta. El plano de deslizamiento normalmente también es compacto o casi compacto.
En los cristales metálicos, el número y tipo de direcciones de deslizamiento y planos de deslizamiento influye en las propiedades del metal. En los metales de estructura cristalina FCC, el esfuerzo cortante resultante crítico es bajo y existe un número óptimo de planos de deslizamiento; en consecuencia, los metales FCC tienden a ser dúctiles. En el caso de los metales BCC, no hay planos compactos disponibles y el esfuerzo cortante resultante crítico es alto; por lo que los metales BCC tienden a ser resistentes. El número de sistemas de deslizamiento en los metales HCP es limitado, haciendo que estos metales se comporten de manera frágil.
Los defectos puntuales, que incluyen vacancias, átomos intersticiales y átomos sustitucionales, introducen campos de esfuerzos de compresión o de tensión que alteran la red adyacente. Como resultado, las dislocaciones no pueden deslizarse en las cercanías de defectos puntuales, incrementándose la resistencia del material. El número de vacancias, o de puntos de red vacíos, depende de la temperatura del material; los átomos intersticiales (localizados en sitios intersticiales entre átomos normales) y los átomos sustitucionales (que remplazan al átomo normal en puntos de la red) a menudo se introducen de manera deliberada y generalmente su número no se altera por los cambios de temperatura del material.
Estas imperfecciones se pueden clasificar en:
- Dislocaciones de cuña.
- Dislocaciones helicoidales o de tornillo.
- Dislocaciones mixtas.
3.5.2.1 Dislocaciones de cuña:
Deslizamiento de los planos cristalinos por acción de una fuerza generada por la inserción de una semiplano adicional de átomos, generando que las dos nuevas superficies sean desplazadas transnacionalmente en dirección normal a la línea de dislocación.
Una dislocación de borde o de cuña se puede ilustrar haciendo un corte parcial en un cristal perfecto, abriendo el cristal y llenando en parte el corte con un plano adicional de átomos. La orilla inferior de este plano insertado representa la dislocación de borde.
 Figura 3.57 Dislocaciones de cuña. [6]
Figura 3.57 Dislocaciones de cuña. [6]
3.5.2.2 Dislocaciones helicoidales o de tornillo:
Se llama así debido a la superficie espiral formada por los planos atómicos alrededor de la línea de dislocación y se forman al aplicar un esfuerzo cizallante. La parte superior de la región frontal del cristal desliza una unidad atómica a la derecha respecto a la parte inferior. En este caso, el vector de Burgers es paralelo al plano que contiene la dislocación y perpendicular al plano de deslizamiento.
La región de distorsión no está bien definida pero alcanza el ancho del diámetro de unos cuantos átomos.
 Figura 3.58 Dislocaciones de tornillo.
Figura 3.58 Dislocaciones de tornillo.
3.5.2.3 Dislocaciones mixtas:
Con frecuencia los cristales exhiben mezcla de las dislocaciones anteriores. Su vector de Burgers no es ni perpendicular ni paralelo a la línea de dislocación, pero mantiene una orientación fija en el espacio.
La estructura atómica local en torno a la dislocación mixta es difícil de visualizar, pero el vector de Burgers proporciona una descripción conveniente y sencilla. Las dislocaciones mixtas tienen componentes de borde y tornillo, con una región de transición entre ellas. Sin embargo, el vector de burgers queda igual para todas las porciones de la dislocación mixta.
Cuando se aplica una fuerza cortante en la dirección del vector de burgers a un cristal que contenga una dislocación, esta se puede mover, rompiendo los enlaces de los átomos en un plano. El plano de corte se desplaza un poco para establecer enlaces con el plano parcial de átomos originales.
El desplazamiento hace que la dislocación se mueva una distancia atómica hacia el lado. Si continua este proceso, la dislocación se mueve a través del cristal hasta que se produce un escalón en el exterior del mismo; el cristal se ha deformado plásticamente.
Otra analogía es el movimiento de avance de una oruga. Levanta alguna de sus patas en determinado momento, y usa el movimiento para ir de un lado a otro, sin levantar todas las patas al mismo tiempo. Una gran diferencia entre el movimiento de una oruga y el de una dislocación es la velocidad con que se mueven. La velocidad con la que se propagan las dislocaciones en los materiales es cercana o mayor que la velocidad del sonido.
Otra forma de visualizar esto es imaginar cómo se movería una onda en una alfombra si tratáramos de eliminarla aplanándola en lugar de levantar la alfombra. Si se pudieran introducir dislocaciones en forma continua en un lado del cristal, moviéndose a través del cristal por la misma trayectoria, el cristal terminaría por quedar cortado a la mitad.
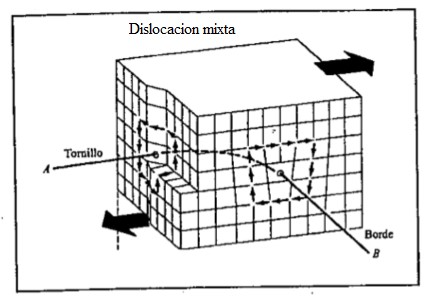 Figura 3.59 Dislocación mixta.
Figura 3.59 Dislocación mixta.
3.5.3. Imperfecciones o defectos superficiales y límites de grano internos:
estos defectos superficiales son límites pueden ser bordes o planos que dividen un material en porciones, cada una de las cuales tiene la misma estructura cristalina, características y propiedades pero en distintas orientaciones cristalográficas. Las dimensiones exteriores del material representan superficies en donde termina el cristal en forma súbita. Cada átomo en la superficie ya no tiene el número adecuado de coordinación y se interrumpe el enlazamiento atómico. Esto es un factor muy importante en la fabricación de dispositivos micro electrónico a base de Si. La superficie exterior también puede ser muy áspera, contener muescas diminutas y ser mucho más reactiva en el interior del material.
Estas imperfecciones se clasifican en:
- Borde de grano o límite de grano.
- Defectos de apilamiento.
3.5.3.1. Borde de grano o límite de grano:
La estructura de muchos materiales cerámicos y metálicos consiste en muchos granos. Un grano es una porción del material dentro de la cual el arreglo de los átomos es casi idéntico. Sin embargo, la orientación del arreglo de átomos, o estructura cristalina, es distinta en cada grano vecino, es decir, en algunas regiones del material existe un desorden estructural, o sea, ocurre un cambio en la orientación cristalográfica como anteriormente se mencionaba; como consecuencia de ello, algunos átomos de la estructura se encuentran más comprimidos y otros más alejados.
Límites de grano de ángulo pequeño: Un límite de grano de ángulo pequeño es un conjunto de dislocaciones que produce una pequeña desorientación entre cristales vecinos. Como la superficie de la energía es menor que la de un límite de grano normal, los límites de grano con ángulo pequeño no son tan eficientes para bloquear los deslizamientos. Los límites de grano con tamaño pequeño que se forman por dislocaciones de borde se llaman límites inclinados los que se forman por dislocaciones de tornillo (véase defectos lineales) se llaman límites de giro.
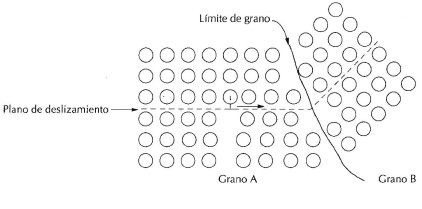 Figura 3.60 Límite de grano. [7]
Figura 3.60 Límite de grano. [7]
3.5.3.2. Defectos de apilamiento:
Se puede observar como la interrupción de la secuencia de apilamiento ordenado de las estructuras cristalinas, es decir, son irregularidades en la frecuencia de los planos cristalinos del material. Estos defectos a su vez se dividen en
- Maclas
- Defectos intrínsecos.
- Defectos extrínsecos.
Maclas: Un límite de macla (o de gemelación) es un plano a través del cual hay una desorientación especial de imagen especular de la estructura cristalina.
Las maclas pueden producirse cuando una fuerza cortante, que actúa a lo largo de límite de macla, que hace que los átomos se desplace de su posición. El maclado sucede durante la deformación o el tratamiento térmico de ciertos metales. Los límites de macla interfieren con el proceso de deslizamiento y aumentan la resistencia del metal. El movimiento de los límites de macla también puede causar la deformación del metal.
Defectos Intrínsecos: naturales, propios del material, salto de los propios átomos.
Defectos Extrínsecos: impurezas, precipitados. [12]
NOTA: Por otra parte existe otra caracterización de algunos materiales en lo que respecta sus propiedades, una de esta son los límites de dominio; los materiales ferro eléctricos son los que desarrollan polarización dieléctrica espontánea y reversible. A los materiales que desarrollan una magnetización en forma parecida se les llama ferromagnéticos o ferromagnéticos. Estos materiales electrónicos y magnéticos contienen dominios. Un dominio es una pequeña región del material cuya dirección de magnetización o polarización dieléctrica permanece igual. En esos materiales se forman muchos dominios pequeños de tal manera que se minimiza la energía libre total del material. En la figura se muestra un ejemplo de dominios en el titanio de bario tetragonal forro eléctrico. La presencia de dominios influye sobre las propiedades dieléctricas y magnéticas de muchos materiales electrónicos y magnéticos. [3]
3.5.4. Defectos tridimensionales macroscópicos. (Volumétricos):
Los defectos volumétricos se forman cuando un grupo de átomos o de defectos puntuales se unen para formar un vacío tridimensional o poro. De manera inversa, un grupo de átomos de alguna impureza puede unirse para formar un precipitado tridimensional. El tamaño de un defecto volumétrico puede variar desde unos cuantos nanómetros hasta centímetros o, en ocasiones, puede ser mayor. Los defectos tienen un efecto o influencia considerable en el comportamiento y desempeño de un material. Finalmente el concepto de un defecto tridimensional o volumétrico puede ampliarse a una región amorfa dentro de un material poli cristalino. Ejemplo, a continuación se muestra un ejemplo de este tipo de defecto volumétrico.
 Figura 3.63 Rocas con porosidades. [11]
Figura 3.63 Rocas con porosidades. [11]
Por ultimo, se mostrará un mapa conceptual (Figura 3.64) en la cual se darán a conocer las distintas imperfecciones posibles presentadas en un material cristalino:
Figura 3.64. Imperfecciones en un material cristalino. [13]
REFERENCIAS.
- F. Smith “FUNDAMENTOS DE LA CIENCIA E INGENIERIA DE LOS MATERIALES”,3rd ed., p.108, 109, 110, 111, 112.University of Central Florida, 1998.
- Átomos intersticiales; recuperado el 13/05/15 de http://ocw.uc3m.es/ciencia-e-oin/quimica-de-los-materiales/Material-de-clase/tema-6.-materiales-metalicos-ceramicos-y-polimeros-i
- Átomo sustitucional; recuperado el 13/05/15 de http://cienciaymateriales.blogspot.com/2013/04/26-defectos-cristalinos-breve.html
- Defecto Frenkel; recuperado el 13/05/15 de http://nelyestradad.blogspot.com/2009_02_01_archive.html
- Defecto Schottky; recuperado el 13/05/15 de http://defectsinsolids.blogspot.com/2010/05/otros-defectos-puntuales-importantes.html
- Dislocaciones de cuña; recuperado el 13/05/15 de http://personales.upv.es/~avicente/curso/unidad3/defectos.html
- Borde de grano o límite de grano; recuperado el 13/05/15 de http://cienciaymateriales.blogspot.com/2013/04/24-como-se-origina-el-borde-de-grano.html
- Defectos de apilamiento; recuperadoel 13/05/15 de http://polaris.esfm.ipn.mx/~fcruz/ADR/Cristalografia/DEFECTOS%20INTERFACIALES%20O%20SUPERFICIALES_2006.pdf
- Maclas; recuperado el 13/05/15 de http://cienciaymateriales.blogspot.com/2013/04/26-defectos-cristalinos-breve.html
- Porosidad ; recuperado el 13/05/15 de http://imgbuddy.com/porosidad-en-fisica.asp
- Rocas con porosidades; recuperado el 13/05/15 de http://www.ehowenespanol.com/cuales-son-rocas-mayor-porosidad-info_238910/
- Defectos intrinsecos y extrinsecos: http://www.academia.edu/8161146/Defecto_cristalino.
- Imperfecciones en mateiales: http://grupoorion.unex.es:8001/rid=1HVQYCY3H-XC7B5Z-4MXG/Imperfecciones%20en%20materiales%20cristalinosfinal(Esther).cmap
Artículos de interés:
- El cristal, la red tridimensional natural de difracción*
- Desarrollo de la cristalografía estructural en el siglo XX. Su impacto en las ciencias biomédicas y las perspectivas en este campo
- Análisis de perfiles de difracción de rayos X de dos materiales metálicos
CRÉDITOS
Recopilación y edición realizada por: Juan Diego Valencia Escarria, Héctor Julián Arias López, Oscar Ipial Fuertes, estudiantes de ingeniería mecánica de la universidad Tecnológica de Pereira 2012.
Modificación realizada por: Miguel Ángel Muñoz Muñoz, Juan Esteban Marulanda López, Sebastián Castiblanco García, Roy Eli Quesada.
– Modificación y organización realizada por: Andres Felipe Romero, Oscar Edwardo Acevedo y Mario Martínez. Estudiantes de Ingeniería Mecánica de la Universidad Tecnológica de Pereira. Intersemestral 2015 1

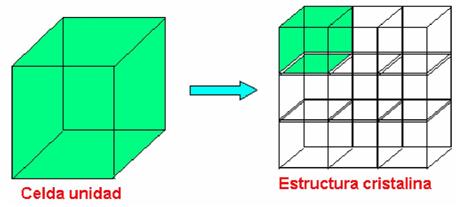
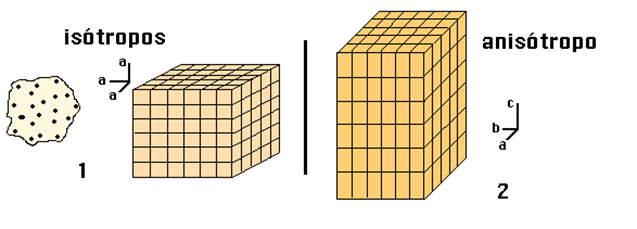



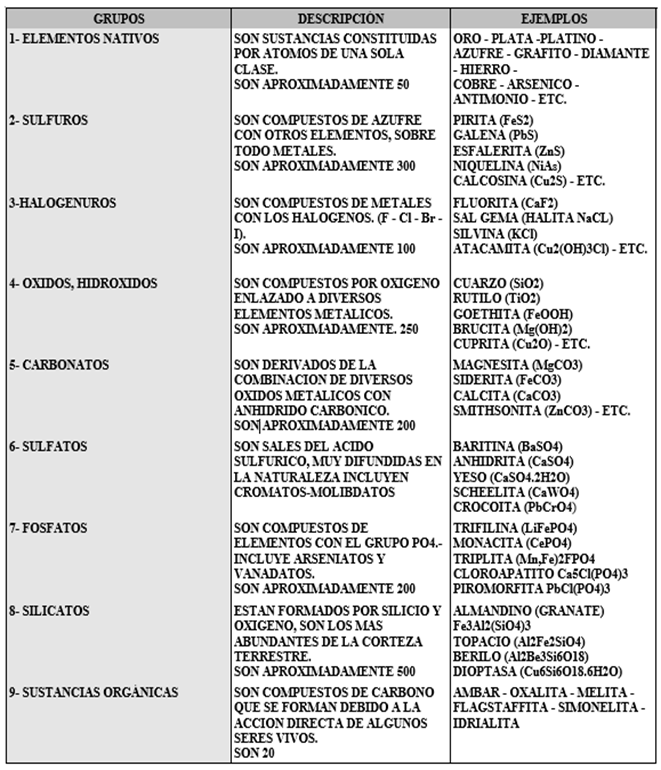




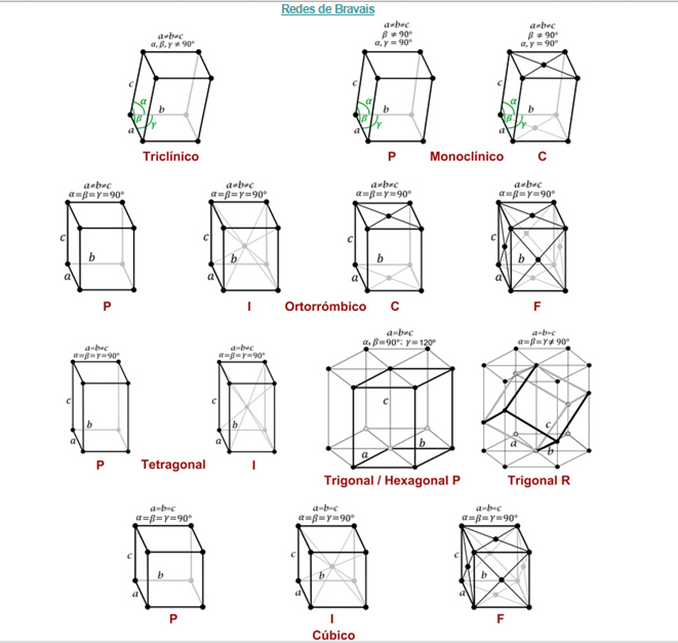


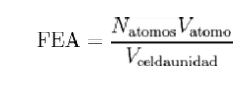






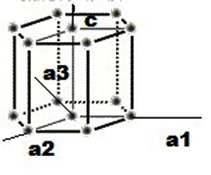
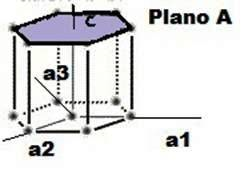

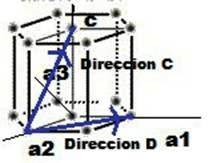



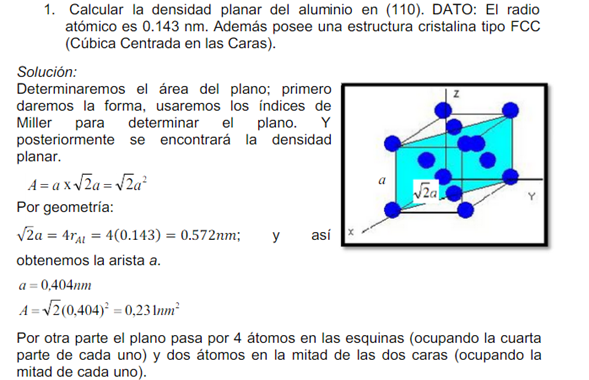
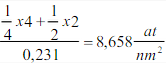
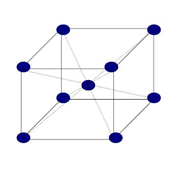
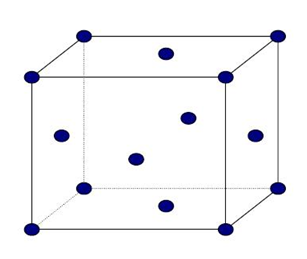

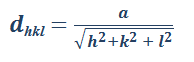
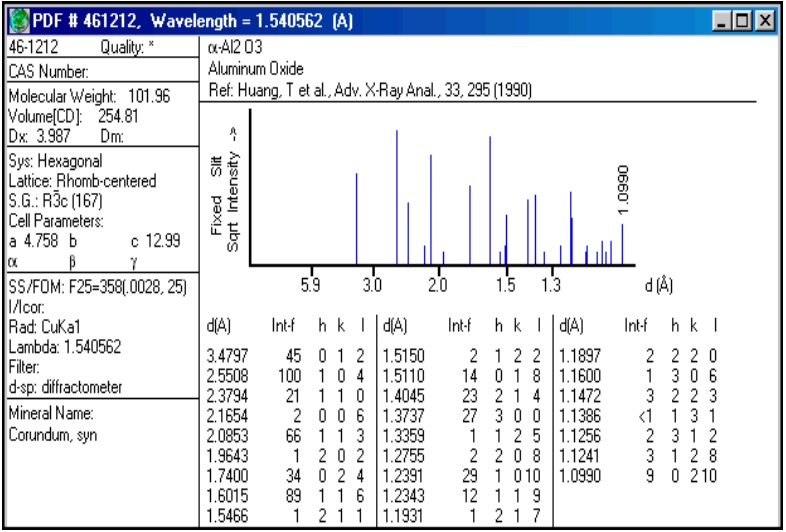
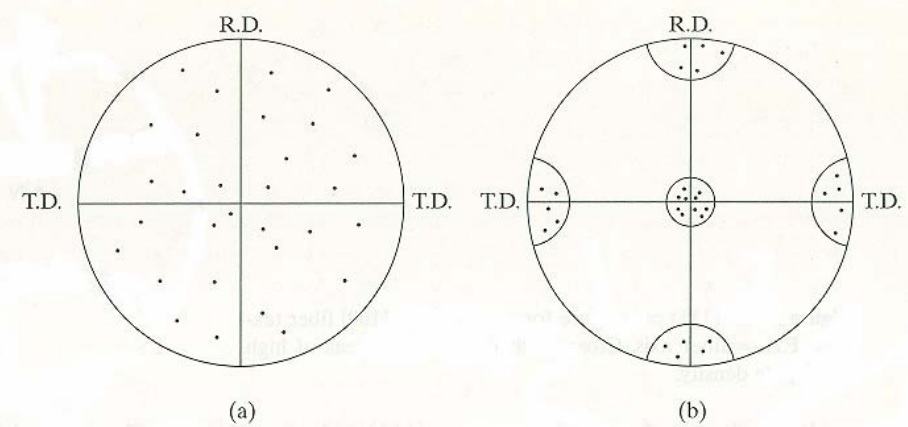
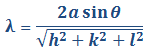


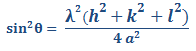

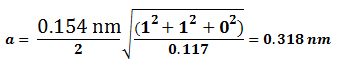
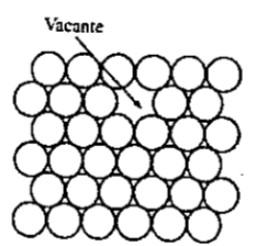



Exelente trabajo me sirvio muchisimo !!! gracias