The increasing demand for customized products with short life cycles and rapid delivery requirements has driven industries to adopt Robotics Assembly Systems (RAS) as a solution to these challenges. An RAS is an integrated manufacturing environment composed of one or multiple workstations capable of assembling diverse product types, interconnected through a material handling system, and coordinated by a centralized control unit. An RAS can be designed in various configurations: Robotic Assembly Lines (RAL), Robotic Assembly Cell (RAC) with one or multiple robots, and, more recently, a configuration known as the Robotic Matrix-Structure Assembly System (RMSAS) has emerged.
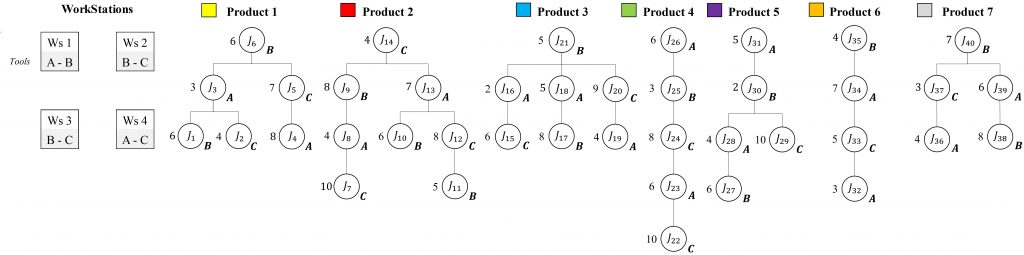
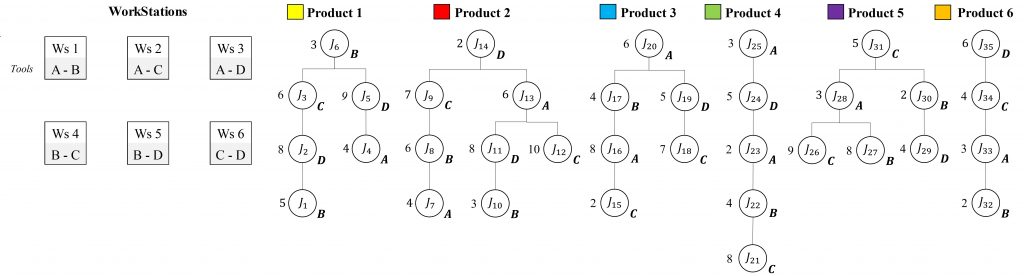
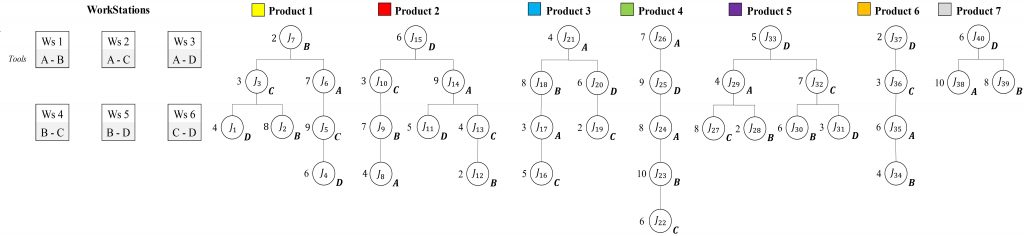
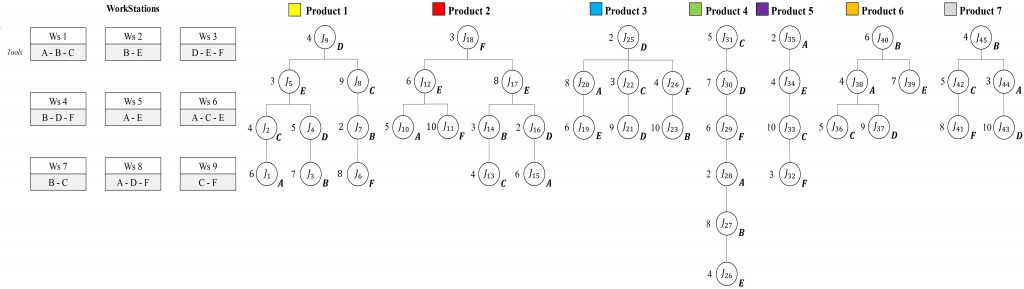
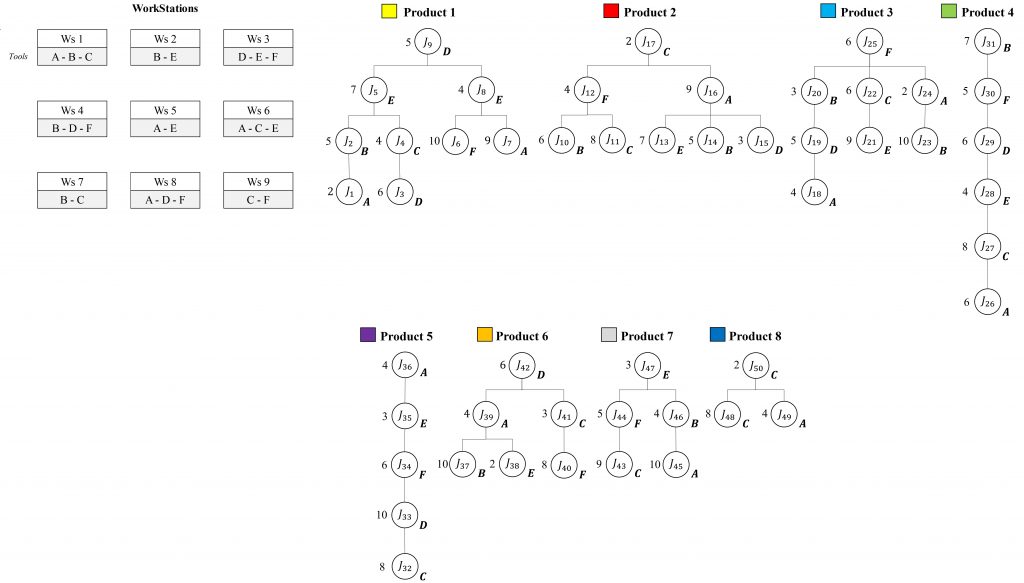
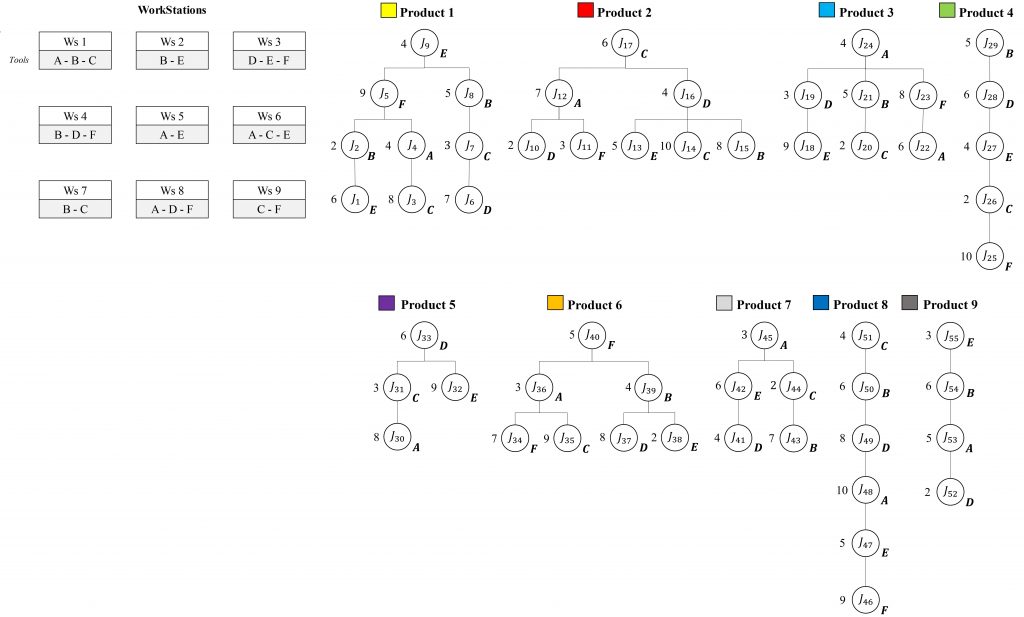
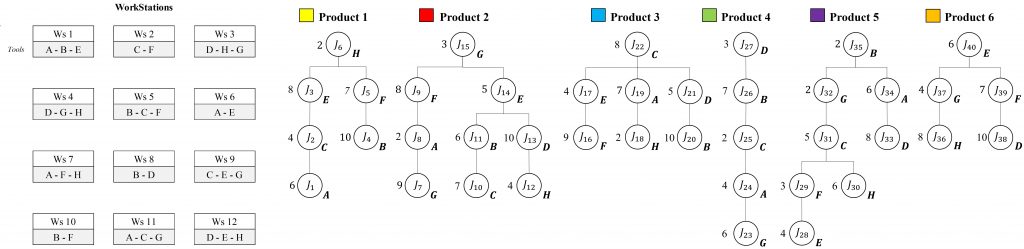
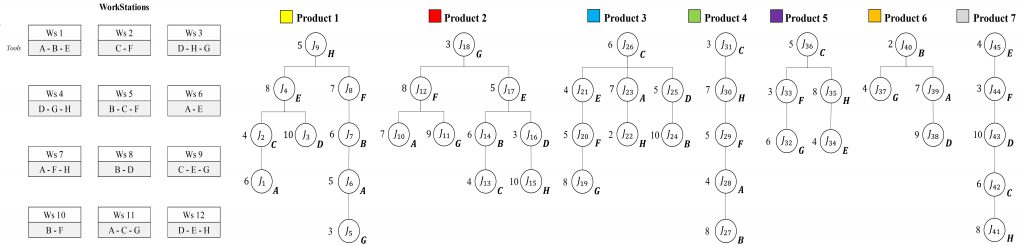
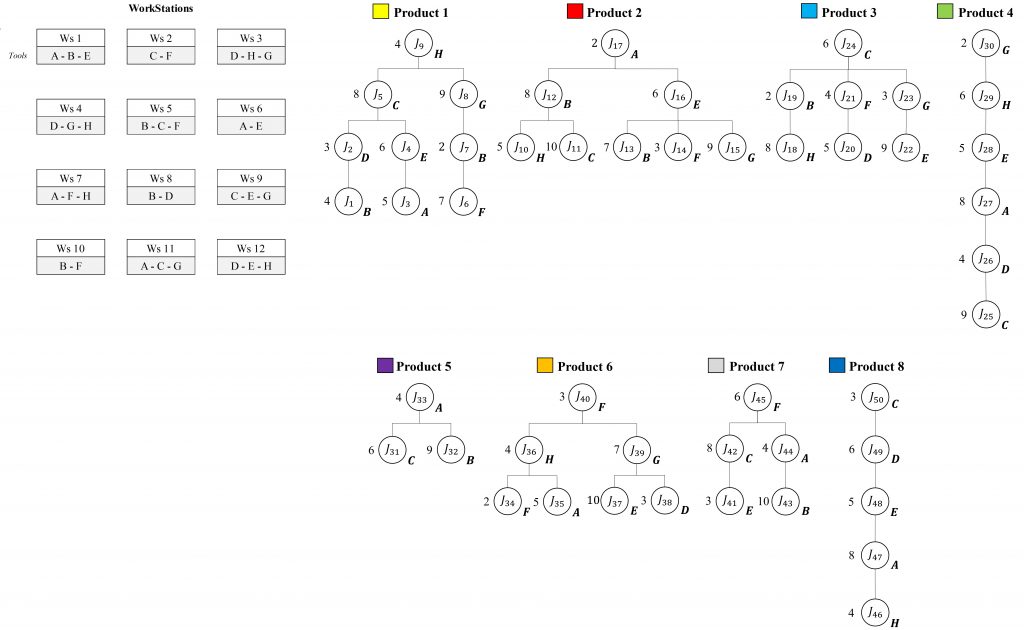
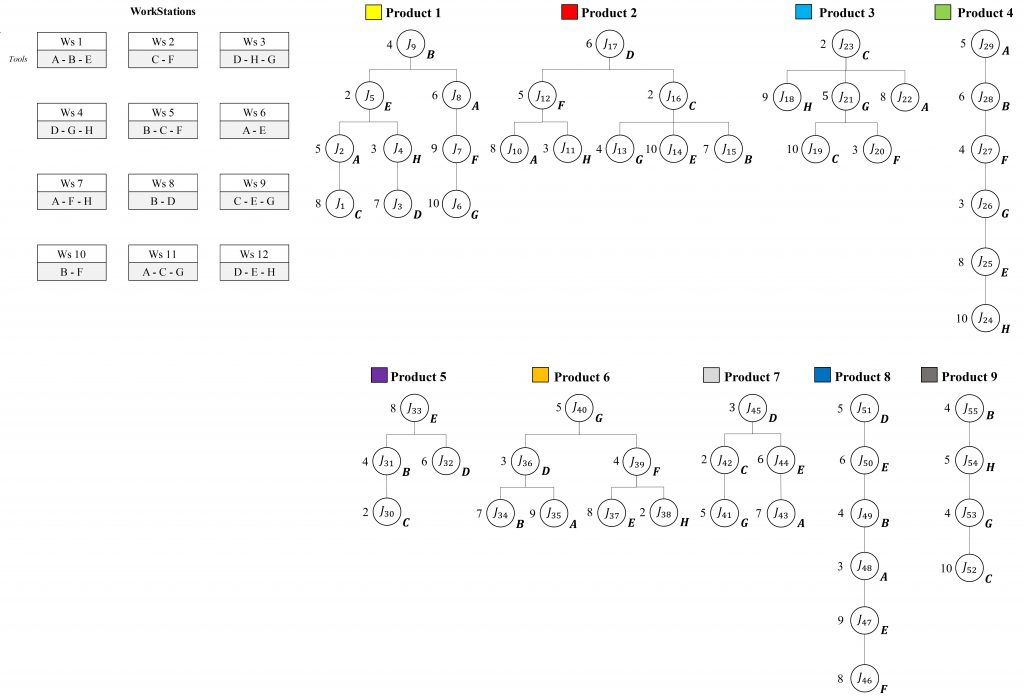
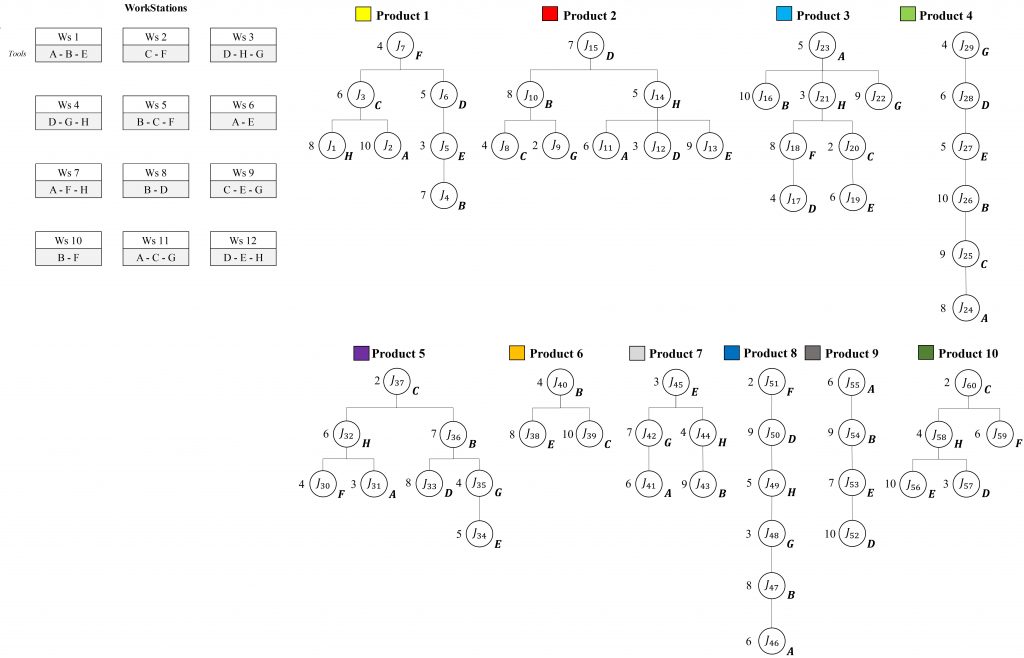
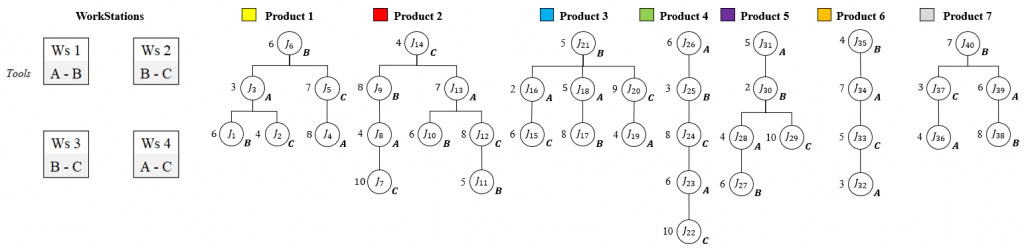
P=[1, 2,…,|P|] be the set of product types. Jp=[J1p, J2p,…,Jnp] the ordered set of assembly tasks required to produce product p ∈ P, where n denotes the total number of tasks for product p. M=[1, 2,…,|M|] the set of available assembly workstations. Each assembly task Jjpcorresponds to a set of operations required for product p. A workstation m ∈ M can execute only a subset of tasks, depending on its technological capabilities. This relationship is defined by the feasibility set:
Φ(Jjp) ⊆ M, ∀Jjp ∈ Jp, p ∈ P
Where Φ (Jjp) denotes the set of workstations capable of processing task Jjp. Since the RMSAS is designed to handle multiple product types, every product must have at least one feasible workstation for each of its tasks:
Φ(Jjp) ≠ ∅, ∀Jjp ∈ Jp, p ∈ P
Conversely, a workstation mmm can process tasks from different products, represented as:
Ψ(m) = {Jjp ∈ Jp ∣ m ∈ Φ(Jjp), p ∈ P}
Where Ψ(m) is the set of tasks executable at workstation m. Thus, the assignment of tasks to workstations is determined by the intersection between product requirements and workstation capabilities, with each Ψ(m) representing only a fraction of the global task set across all products.
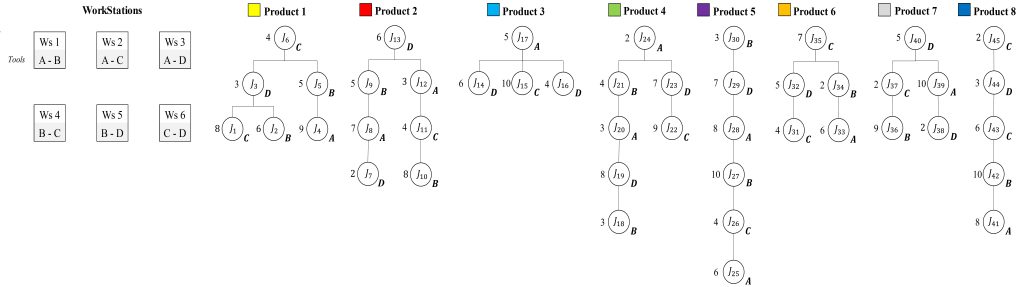
Instances:
Group I
The execution of assembly operations by industrial robots tends to exhibit consistent and low variability across multiple runs. In contrast, stochastic processing times are typically associated with scenarios involving human–robot interaction within the same assembly system. Some studies suggest that processing times can be modeled using a uniform probability distribution; however, the range of this distribution may vary depending on the type of assembly task being analyzed. For example, processing times in the electronics industry are usually short—often measured in seconds—while in the automotive industry, assembly tasks tend to be longer, typically measured in minutes. Based on this distinction, the present study evaluates each instance under two different processing time scenarios. For Group_I of products, task durations are modeled using a uniform distribution in the range [2-10] time units, representing short-cycle tasks.
Matrix-Structure 2 x 2
Int_1
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
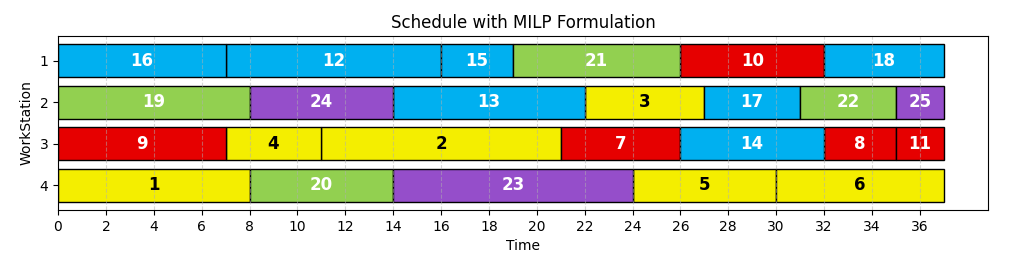
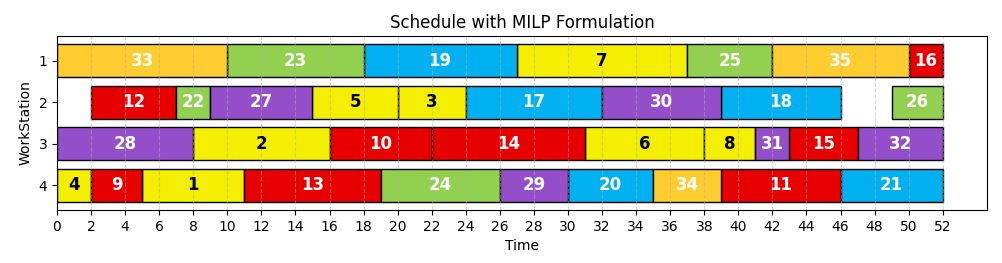
| Tasks Ws1 Ws2 Ws3 Ws4 1 4 4 1000 4 2 1000 2 2 1000 3 5 1000 5 5 4 6 6 1000 6 5 1000 4 4 1000 6 5 1000 5 5 7 1000 10 10 1000 8 4 4 1000 4 9 1000 8 8 1000 10 6 1000 6 6 11 4 4 1000 4 12 3 1000 3 3 13 5 5 1000 5 14 1000 7 7 1000 15 4 4 1000 4 16 4 4 1000 4 17 1000 6 6 1000 18 2 1000 2 2 19 1000 8 8 1000 20 5 1000 5 5 | Predecessor Successor 1 3 2 3 3 5 4 5 6 7 8 9 7 11 9 11 10 11 12 13 13 14 14 15 16 17 18 19 17 20 19 20 | WorkStation Product Task Start_Time Completion_Time 1 P1 1 0 4 1 P1 3 4 2 1 P1 4 14 9 1 P3 13 9 20 1 P4 20 22 27 2 P1 2 0 5 2 P2 11 23 15 2 P3 14 16 13 2 P4 17 10 23 2 P4 19 2 23 3 P1 5 23 27 3 P2 7 5 5 3 P2 9 15 14 3 P3 12 2 23 3 P4 18 0 27 4 P2 6 0 9 4 P2 8 9 16 4 P2 10 17 2 4 P3 15 23 10 4 P4 16 5 27 | Makespan = 27 Ws1: Total_Time=25.0, Utilization=0.9259 Ws2: Total_Time=27.0, Utilization=1.0000 Ws3: Total_Time=27.0, Utilization=1.0000 Ws4: Total_Time=23.0, Utilization=0.8519 Average System Utilization: 0.9444 |
Makespan = 27 Run-time = 6,4 seconds
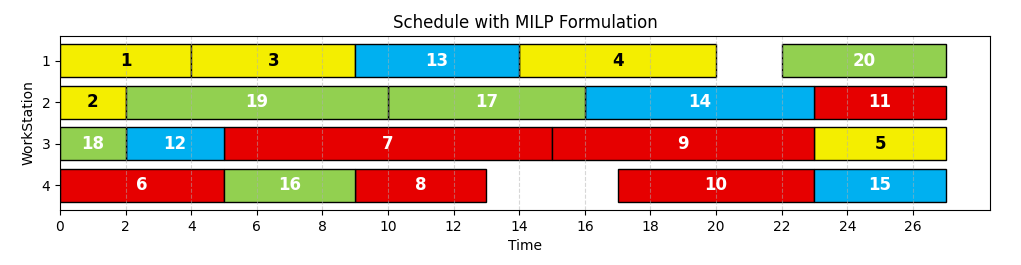
Gantt Chart
Int_2
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 1 8 1000 8 8 2 1000 10 10 10 3 5 5 1000 1000 4 4 1000 4 4 5 1000 6 6 6 6 7 1000 7 7 7 1000 5 5 5 8 3 1000 3 3 9 1000 7 7 7 10 6 6 1000 1000 11 1000 2 2 2 12 9 1000 9 9 13 8 8 1000 1000 14 1000 6 6 6 15 3 1000 3 3 16 7 7 1000 1000 17 1000 4 4 4 18 5 5 1000 1000 19 8 8 1000 1000 20 1000 6 6 6 21 7 1000 7 7 22 4 4 1000 1000 23 10 1000 10 10 24 1000 6 6 6 25 2 2 1000 1000 | Predecessor Successor 1 3 2 3 4 5 3 6 5 6 7 8 9 10 8 11 10 11 12 14 13 14 16 17 14 18 15 18 17 18 19 20 20 21 21 22 23 25 24 25 | WorkStation Product Task Start_Time Completion_Time 1 P2 10 26 8 1 P3 12 7 21 1 P3 15 16 27 1 P3 16 0 11 1 P3 18 32 30 1 P4 21 19 37 2 P1 3 22 26 2 P3 13 14 35 2 P3 17 27 7 2 P4 19 0 32 2 P4 22 31 37 2 P5 24 8 16 2 P5 25 35 22 3 P1 2 11 32 3 P1 4 7 19 3 P2 7 21 7 3 P2 8 32 31 3 P2 9 0 37 3 P2 11 35 8 3 P3 14 26 14 4 P1 1 0 26 4 P1 5 24 35 4 P1 6 30 24 4 P4 20 8 14 4 P5 23 14 37 | Makespan = 37 Ws1: Total_Time=37.0, Utilization=1.0000 Ws2: Total_Time=37.0, Utilization=1.0000 Ws3: Total_Time=37.0, Utilization=1.0000 Ws4: Total_Time=37.0, Utilization=1.0000 Average System Utilization: 1.0000 |
Makespan = 37 Run-time = 15,6 seconds
Gantt Chart
Int_3
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
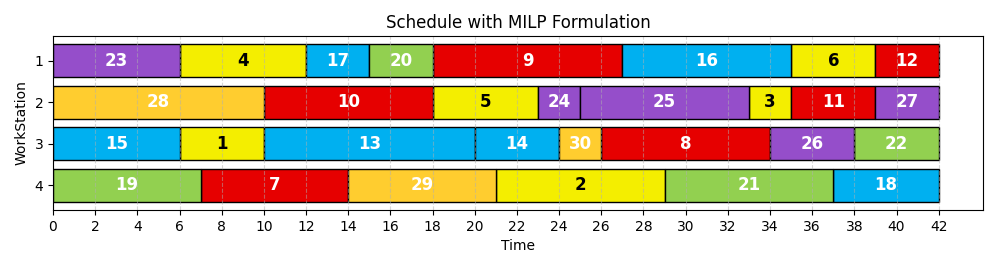
| Tasks Ws1 Ws2 Ws3 Ws4 1 4 1000 4 1000 2 1000 8 8 8 3 2 2 1000 2 4 6 6 1000 6 5 1000 5 5 5 6 4 1000 4 1000 7 1000 7 7 7 8 8 1000 8 1000 9 9 1000 9 1000 10 8 8 1000 8 11 1000 4 4 4 12 3 3 1000 3 13 1000 10 10 10 14 4 1000 4 1000 15 1000 6 6 6 16 8 1000 8 1000 17 3 3 1000 3 18 5 5 1000 5 19 7 7 1000 7 20 3 1000 3 1000 21 1000 8 8 8 22 4 1000 4 1000 23 6 1000 6 1000 24 2 2 1000 2 25 1000 8 8 8 26 4 1000 4 1000 27 1000 3 3 3 28 1000 10 10 10 29 7 7 1000 7 30 2 1000 2 1000 | Predecessor Successor 1 2 2 3 4 5 3 6 5 6 7 8 9 11 10 11 8 12 11 12 14 16 15 16 13 18 16 18 17 18 19 20 20 21 21 22 23 24 25 26 24 27 26 27 28 29 29 30 | WorkStation Product Task Start_Time Completion_Time 1 P1 4 6 10 1 P1 6 35 29 1 P2 9 18 35 1 P2 12 39 12 1 P3 16 27 23 1 P3 17 12 39 1 P4 20 15 14 1 P5 23 0 34 2 P1 3 33 27 2 P1 5 18 18 2 P2 10 10 39 2 P2 11 35 42 2 P5 24 23 20 2 P5 25 25 24 2 P5 27 39 6 2 P6 28 0 35 3 P1 1 6 15 3 P2 8 26 42 3 P3 13 10 7 3 P3 14 20 18 3 P3 15 0 37 3 P4 22 38 42 3 P5 26 34 6 3 P6 30 24 25 4 P1 2 21 33 4 P2 7 7 38 4 P3 18 37 42 4 P4 19 0 10 4 P4 21 29 21 4 P6 29 14 26 | Makespan = 42 Ws1: Total_Time=42.0, Utilization=1.0000 Ws2: Total_Time=42.0, Utilization=1.0000 Ws3: Total_Time=42.0, Utilization=1.0000 Ws4: Total_Time=42.0, Utilization=1.0000 Average System Utilization: 1.0000 |
Makespan = 42 Run-time = 76,1 seconds
Gantt Chart
Int_4
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 1 6 1000 1000 6 2 1000 8 8 8 3 4 4 4 1000 4 2 1000 1000 2 5 5 5 5 1000 6 1000 7 7 7 7 10 1000 1000 10 8 3 3 3 1000 9 3 1000 1000 3 10 6 6 6 1000 11 1000 7 7 7 12 5 5 5 1000 13 8 1000 1000 8 14 1000 9 9 9 15 4 4 4 1000 16 2 1000 1000 2 17 1000 8 8 8 18 7 7 7 1000 19 9 1000 1000 9 20 1000 5 5 5 21 6 1000 1000 6 22 1000 2 2 2 23 8 8 8 1000 24 7 1000 1000 7 25 5 5 5 1000 26 1000 3 3 3 27 1000 6 6 6 28 8 8 8 1000 29 4 1000 1000 4 30 1000 7 7 7 31 2 2 2 1000 32 1000 5 5 5 33 10 1000 1000 10 34 1000 4 4 4 35 8 8 8 1000 | Predecessor Successor 1 3 2 3 4 5 5 6 3 8 6 8 7 8 9 10 10 11 12 13 13 15 14 15 11 16 15 16 17 18 19 20 18 21 20 21 22 23 23 24 24 25 25 26 27 29 28 29 30 31 29 32 31 32 33 34 34 35 | WorkStation Product Task Start_Time Completion_Time 1 P1 7 27 11 1 P2 16 50 16 1 P3 19 18 24 1 P4 23 10 2 1 P4 25 37 20 1 P6 33 0 38 1 P6 35 42 37 2 P1 3 20 41 2 P1 5 15 5 2 P2 12 2 22 2 P3 17 24 46 2 P3 18 39 7 2 P4 22 7 19 2 P4 26 49 31 2 P5 27 9 47 2 P5 30 32 52 3 P1 2 8 32 3 P1 6 31 46 3 P1 8 38 27 3 P2 10 16 35 3 P2 14 22 52 3 P2 15 43 9 3 P5 28 0 18 3 P5 31 41 26 3 P5 32 47 42 4 P1 1 5 52 4 P1 4 0 15 4 P2 9 2 8 4 P2 11 39 30 4 P2 13 11 39 4 P3 20 30 43 4 P3 21 46 52 4 P4 24 19 10 4 P5 29 26 39 4 P6 34 35 50 | Makespan = 52 Ws1: Total_Time=52.0, Utilization=1.0000 Ws2: Total_Time=47.0, Utilization=0.9038 Ws3: Total_Time=52.0, Utilization=1.0000 Ws4: Total_Time=52.0, Utilization=1.0000 Average System Utilization: 0.9760 |
Makespan = 52 Run-time = 136 seconds
Gantt Chart
Int_5
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 1 6 6 6 1000 2 1000 4 4 4 3 3 1000 1000 3 4 8 1000 1000 8 5 1000 7 7 7 6 6 6 6 1000 7 1000 10 10 10 8 4 1000 1000 4 9 8 8 8 1000 10 6 6 6 1000 11 5 5 5 1000 12 1000 8 8 8 13 7 1000 1000 7 14 1000 4 4 4 15 1000 6 6 6 16 2 1000 1000 2 17 8 8 8 1000 18 5 1000 1000 5 19 4 1000 1000 4 20 1000 9 9 9 21 5 5 5 1000 22 1000 10 10 10 23 6 1000 1000 6 24 1000 8 8 8 25 3 3 3 1000 26 6 1000 1000 6 27 6 6 6 1000 28 4 1000 1000 4 29 1000 10 10 10 30 2 2 2 1000 31 5 1000 1000 5 32 3 1000 1000 3 33 1000 5 5 5 34 7 1000 1000 7 35 4 4 4 1000 36 4 1000 1000 4 37 1000 3 3 3 38 8 8 8 1000 39 6 1000 1000 6 40 7 7 7 1000 | Predecessor Successor 1 3 2 3 4 5 3 6 5 6 7 8 8 9 11 12 10 13 12 13 9 14 13 14 15 16 17 18 19 20 16 21 18 21 20 21 22 23 23 24 24 25 25 26 27 28 28 30 29 30 30 31 32 33 33 34 34 35 36 37 38 39 37 40 39 40 | WorkStation Product Task Start_Time Completion_Time 1 P7 38 0 30 1 P3 19 8 33 1 P2 8 12 38 1 P3 18 16 35 1 P2 10 21 42 1 P1 4 27 48 1 P1 3 35 12 1 P3 16 38 16 1 P7 39 40 24 1 P6 34 46 27 1 P4 26 53 5 2 P2 7 2 26 2 P5 27 12 52 2 P2 12 18 59 2 P3 20 26 10 2 P1 5 35 40 2 P1 6 42 16 2 P5 30 48 21 2 P3 21 50 12 2 P6 35 55 35 3 P2 11 0 55 3 P7 37 5 23 3 P3 17 8 29 3 P2 9 16 45 3 P1 1 24 48 3 P5 29 30 59 3 P6 33 40 18 3 P4 25 45 37 3 P7 40 48 40 3 P2 14 55 50 4 P7 36 0 57 4 P3 15 4 13 4 P6 32 10 45 4 P4 22 13 53 4 P4 23 23 59 4 P1 2 29 4 4 P5 28 33 8 4 P4 24 37 8 4 P2 13 45 46 4 P5 31 52 55 | Makespan = 59 Ws1: Total_Time=59.0, Utilization=1.0000 Ws2: Total_Time=57.0, Utilization=0.9661 Ws3: Total_Time=59.0, Utilization=1.0000 Ws4: Total_Time=57.0, Utilization=0.9661 Average System Utilization: 0.9831 |
Makespan = 59 Run-time = 2467 seconds
Gantt Chart

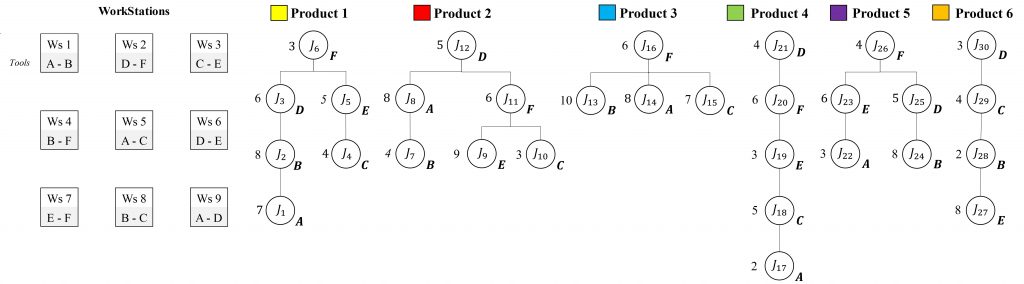
Matrix-Structure 2 x 3
Int_6

| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 1 1000 1000 6 1000 6 6 2 1000 7 1000 7 1000 7 3 8 1000 1000 8 8 1000 4 4 4 4 1000 1000 1000 5 1000 1000 10 1000 10 10 6 5 5 5 1000 1000 1000 7 1000 3 1000 3 1000 3 8 1000 1000 5 1000 5 5 9 4 4 4 1000 1000 1000 10 1000 10 1000 10 1000 10 11 7 1000 1000 7 7 1000 12 1000 1000 6 1000 6 6 13 7 1000 1000 7 7 1000 14 9 9 9 1000 1000 1000 15 1000 2 1000 2 1000 2 16 1000 1000 4 1000 4 4 17 1000 9 1000 9 1000 9 18 1000 1000 5 1000 5 5 19 6 6 6 1000 1000 1000 20 3 1000 1000 3 3 1000 21 1000 3 1000 3 1000 3 22 6 1000 1000 6 6 1000 23 8 1000 1000 8 8 1000 24 7 7 7 1000 1000 1000 25 1000 2 1000 2 1000 2 | Predecessor Successor 1 3 2 3 4 5 3 6 5 6 7 8 8 9 9 11 10 11 12 13 13 16 14 16 15 16 17 18 18 19 19 20 21 22 23 24 22 25 24 25 | WorkStation Product Task Start_Time Completion_Time 1 P1 4 0 6 1 P3 14 4 8 1 P3 13 13 16 1 P1 6 20 4 2 P4 17 0 19 2 P5 21 9 25 2 P2 9 12 3 2 P4 19 16 11 2 P5 25 23 16 3 P1 1 0 18 3 P2 8 6 25 3 P4 18 11 9 3 P5 24 16 20 4 P1 2 1 13 4 P2 10 8 21 4 P2 11 18 25 5 P5 23 0 9 5 P1 3 8 16 5 P5 22 16 22 5 P4 20 22 25 6 P2 7 0 12 6 P3 12 3 22 6 P1 5 9 8 6 P3 15 19 23 6 P3 16 21 25 | Makespan = 25 Ws1: Total_Time=25.0, Utilization=1.0000 Ws2: Total_Time=24.0, Utilization=0.9600 Ws3: Total_Time=23.0, Utilization=0.9200 Ws4: Total_Time=24.0, Utilization=0.9600 Ws5: Total_Time=25.0, Utilization=1.0000 Ws6: Total_Time=25.0, Utilization=1.0000 Average System Utilization: 0.9733 |
Makespan = 25 Run-time = 18,8 seconds
Gantt Chart

Int_7

| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 1 1000 1000 7 1000 7 7 2 5 5 5 1000 1000 1000 3 3 1000 1000 3 3 1000 4 1000 1000 8 1000 8 8 5 1000 4 1000 4 1000 4 6 6 6 6 1000 1000 1000 7 1000 2 1000 2 1000 2 8 10 1000 1000 10 10 1000 9 1000 5 1000 5 1000 5 10 1000 1000 6 1000 6 6 11 4 4 4 1000 1000 1000 12 1000 1000 9 1000 9 9 13 3 1000 1000 3 3 1000 14 1000 1000 7 1000 7 7 15 1000 2 1000 2 1000 2 16 8 8 8 1000 1000 1000 17 4 1000 1000 4 4 1000 18 1000 1000 5 1000 5 5 19 6 1000 1000 6 6 1000 20 5 5 5 1000 1000 1000 21 1000 8 1000 8 1000 8 22 1000 1000 9 1000 9 9 23 2 2 2 1000 1000 1000 24 9 9 9 1000 1000 1000 25 6 1000 1000 6 6 1000 26 1000 3 1000 3 1000 3 27 1000 1000 4 1000 4 4 28 1000 10 1000 10 1000 10 29 7 1000 1000 7 7 1000 30 6 6 6 1000 1000 1000 | Predecessor Successor 1 3 2 3 4 5 5 6 3 7 6 7 9 10 8 11 10 11 11 13 12 13 14 15 15 18 16 18 17 18 19 20 20 21 21 22 22 23 25 26 24 27 26 27 28 29 29 30 | WorkStation Product Task Start_Time Completion_Time 1 P5 25 0 19 1 P4 20 6 24 1 P5 24 11 27 1 P1 6 22 8 2 P2 9 0 12 2 P6 28 5 28 2 P2 11 15 30 2 P1 2 19 11 2 P6 30 24 5 3 P2 12 0 15 3 P2 10 9 19 3 P3 16 15 9 3 P5 27 24 30 3 P4 23 28 17 4 P2 8 1 24 4 P4 21 11 23 4 P5 26 19 10 4 P3 15 22 30 4 P1 3 24 6 4 P2 13 27 11 5 P4 19 0 19 5 P3 17 6 28 5 P3 14 10 30 5 P6 29 17 20 5 P3 18 25 6 6 P1 4 0 22 6 P1 5 8 28 6 P1 1 12 15 6 P4 22 19 24 6 P1 7 28 30 | Makespan = 30 Ws1: Total_Time=26.0, Utilization=0.8667 Ws2: Total_Time=30.0, Utilization=1.0000 Ws3: Total_Time=29.0, Utilization=0.9667 Ws4: Total_Time=29.0, Utilization=0.9667 Ws5: Total_Time=29.0, Utilization=0.9667 Ws6: Total_Time=30.0, Utilization=1.0000 Average System Utilization: 0.9611 |
Makespan = 30 Run-time = 82,3 seconds
Gantt Chart

Int_8
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 1 5 1000 1000 5 5 1000 2 1000 1000 8 1000 8 8 3 1000 6 1000 6 1000 6 4 4 4 4 1000 1000 1000 5 1000 1000 9 1000 9 9 6 3 1000 1000 3 3 1000 7 4 4 4 1000 1000 1000 8 6 1000 1000 6 6 1000 9 1000 7 1000 7 1000 7 10 3 1000 1000 3 3 1000 11 1000 1000 8 1000 8 8 12 1000 10 1000 10 1000 10 13 6 6 6 1000 1000 1000 14 1000 1000 2 1000 2 2 15 1000 2 1000 2 1000 2 16 8 8 8 1000 1000 1000 17 4 1000 1000 4 4 1000 18 1000 7 1000 7 1000 7 19 1000 1000 5 1000 5 5 20 6 6 6 1000 1000 1000 21 1000 8 1000 8 1000 8 22 4 1000 1000 4 4 1000 23 2 2 2 1000 1000 1000 24 1000 1000 5 1000 5 5 25 3 3 3 1000 1000 1000 26 1000 9 1000 9 1000 9 27 8 1000 1000 8 8 1000 28 3 3 3 1000 1000 1000 29 1000 1000 4 1000 4 4 30 2 1000 1000 2 2 1000 31 1000 5 1000 5 1000 5 32 2 1000 1000 2 2 1000 33 3 3 3 1000 1000 1000 34 1000 4 1000 4 1000 4 35 1000 1000 6 1000 6 6 | Predecessor Successor 1 2 2 3 4 5 3 6 5 6 7 8 8 9 10 11 11 13 12 13 9 14 13 14 15 16 16 17 18 19 17 20 19 20 21 22 22 23 23 24 24 25 26 28 27 28 29 30 28 31 30 31 32 33 33 34 34 35 | WorkStation Product Task Start_Time Completion_Time 1 P1 4 0 5 1 P1 6 28 13 1 P2 13 22 20 1 P3 16 4 4 1 P4 23 20 22 1 P5 27 12 31 2 P2 9 21 5 2 P3 15 0 11 2 P3 18 11 28 2 P4 21 2 3 2 P4 25 28 11 2 P6 33 18 10 3 P1 2 5 28 3 P1 5 13 30 3 P2 7 1 2 3 P3 20 25 12 3 P5 28 22 21 4 P1 1 0 18 4 P2 8 5 25 4 P5 26 12 31 4 P5 31 26 10 4 P6 34 21 15 5 P2 10 0 22 5 P2 11 3 28 5 P2 14 28 31 5 P3 17 17 21 5 P4 22 11 20 5 P4 24 23 25 5 P5 30 21 14 5 P6 32 15 23 6 P1 3 14 31 6 P2 12 0 17 6 P3 19 20 21 6 P5 29 10 25 6 P6 35 25 31 | Makespan = 31 Ws1: Total_Time=31.0, Utilization=1.0000 Ws2: Total_Time=30.0, Utilization=0.9677 Ws3: Total_Time=30.0, Utilization=0.9677 Ws4: Total_Time=29.0, Utilization=0.9355 Ws5: Total_Time=30.0, Utilization=0.9677 Ws6: Total_Time=31.0, Utilization=1.0000 Average System Utilization: 0.9731 |
Makespan = 31 Run-time = 546 seconds
Gantt Chart

Int_9
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 1 1000 1000 4 1000 4 4 2 8 1000 1000 8 8 1000 3 1000 3 1000 3 1000 3 4 1000 1000 6 1000 6 6 5 1000 9 1000 9 1000 9 6 7 7 7 1000 1000 1000 7 2 1000 1000 2 2 1000 8 4 4 4 1000 1000 1000 9 7 1000 1000 7 7 1000 10 1000 3 1000 3 1000 3 11 1000 1000 5 1000 5 5 12 2 1000 1000 2 2 1000 13 1000 4 1000 4 1000 4 14 9 9 9 1000 1000 1000 15 1000 1000 6 1000 6 6 16 1000 5 1000 5 1000 5 17 3 3 3 1000 1000 1000 18 8 1000 1000 8 8 1000 19 1000 2 1000 2 1000 2 20 1000 1000 6 1000 6 6 21 4 4 4 1000 1000 1000 22 1000 6 1000 6 1000 6 23 10 1000 1000 10 10 1000 24 8 8 8 1000 1000 1000 25 1000 1000 9 1000 9 9 26 7 7 7 1000 1000 1000 27 1000 8 1000 8 1000 8 28 2 1000 1000 2 2 1000 29 4 4 4 1000 1000 1000 30 6 1000 1000 6 6 1000 31 1000 1000 3 1000 3 3 32 1000 7 1000 7 1000 7 33 1000 1000 5 1000 5 5 34 4 1000 1000 4 4 1000 35 6 6 6 1000 1000 1000 36 1000 3 1000 3 1000 3 37 1000 1000 2 1000 2 2 38 10 10 10 1000 1000 1000 39 8 1000 1000 8 8 1000 40 1000 1000 6 1000 6 6 | Predecessor Successor 1 3 2 3 4 5 5 6 3 7 6 7 8 9 9 10 11 14 12 13 13 14 10 15 14 15 16 17 17 18 19 20 18 21 20 21 22 23 23 24 24 25 25 26 27 29 28 29 30 32 31 32 29 33 32 33 34 35 35 36 36 37 38 40 39 40 | WorkStation Product Task Start_Time Completion_Time 1 P7 38 0 18 1 P6 34 10 36 1 P4 24 17 39 1 P2 14 25 6 1 P1 7 39 17 2 P5 27 0 30 2 P1 5 8 41 2 P6 35 17 22 2 P1 6 23 29 2 P3 21 30 35 2 P4 26 34 17 3 P1 4 0 6 3 P3 17 6 10 3 P5 29 9 34 3 P1 1 14 41 3 P2 8 18 5 3 P4 25 25 9 3 P2 15 35 28 4 P3 16 0 12 4 P5 28 6 23 4 P7 39 8 34 4 P5 30 16 6 4 P2 9 22 17 4 P5 32 29 25 4 P1 3 36 34 5 P2 12 4 41 5 P4 23 7 8 5 P3 18 20 8 5 P1 2 28 13 5 P5 33 36 22 6 P4 22 0 26 6 P2 13 6 36 6 P3 19 10 41 6 P2 11 12 14 6 P3 20 17 23 6 P5 31 23 38 6 P7 40 26 41 6 P2 10 32 10 6 P6 36 35 16 6 P6 37 39 32 | Makespan = 41 Ws1: Total_Time=33.0, Utilization=0.8049 Ws2: Total_Time=41.0, Utilization=1.0000 Ws3: Total_Time=36.0, Utilization=0.8780 Ws4: Total_Time=38.0, Utilization=0.9268 Ws5: Total_Time=33.0, Utilization=0.8049 Ws6: Total_Time=40.0, Utilization=0.9756 Average System Utilization: 0.8984 |
Makespan = 41 Run-time = 1001 seconds
Gantt Chart

Int_10
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 1 1000 8 1000 8 1000 8 2 6 1000 1000 6 6 1000 3 1000 1000 3 1000 3 3 4 9 9 9 1000 1000 1000 5 5 1000 1000 5 5 1000 6 1000 4 1000 4 1000 4 7 1000 1000 9 1000 9 9 8 7 7 7 1000 1000 1000 9 5 1000 1000 5 5 1000 10 8 1000 1000 8 8 1000 11 1000 4 1000 4 1000 4 12 3 3 3 1000 1000 1000 13 1000 1000 6 1000 6 6 14 1000 1000 6 1000 6 6 15 1000 10 1000 10 1000 10 16 1000 1000 9 1000 9 9 17 5 5 5 1000 1000 1000 18 6 1000 1000 6 6 1000 19 1000 1000 8 1000 8 8 20 3 3 3 1000 1000 1000 21 4 1000 1000 4 4 1000 22 1000 9 1000 9 1000 9 23 1000 1000 7 1000 7 7 24 2 2 2 1000 1000 1000 25 6 6 6 1000 1000 1000 26 1000 4 1000 4 1000 4 27 10 1000 1000 10 10 1000 28 8 8 8 1000 1000 1000 29 1000 1000 7 1000 7 7 30 3 1000 1000 3 3 1000 31 1000 4 1000 4 1000 4 32 1000 1000 5 1000 5 5 33 6 6 6 1000 1000 1000 34 10 1000 1000 10 10 1000 35 1000 7 1000 7 1000 7 36 9 1000 1000 9 9 1000 37 1000 2 1000 2 1000 2 38 1000 1000 8 1000 8 8 39 10 10 10 1000 1000 1000 40 1000 1000 5 1000 5 5 41 8 8 8 1000 1000 1000 42 10 1000 1000 10 10 1000 43 1000 6 1000 6 1000 6 44 1000 1000 7 1000 7 7 45 1000 5 1000 5 1000 5 | Predecessor Successor 1 3 2 3 4 5 3 6 5 6 7 8 8 9 10 11 11 12 9 13 12 13 14 17 15 17 16 17 18 19 19 20 20 21 22 23 21 24 23 24 25 26 26 27 27 28 28 29 29 30 31 32 33 34 32 35 34 35 36 37 38 39 37 40 39 40 41 42 42 43 43 44 44 45 | WorkStation Product Task Start_Time Completion_Time 1 P5 25 0 30 1 P7 39 6 16 1 P7 36 16 38 1 P2 8 25 11 1 P2 9 32 37 1 P4 21 37 44 1 P4 24 42 8 2 P1 4 2 32 2 P3 15 11 37 2 P2 11 21 8 2 P7 37 25 25 2 P6 35 27 37 2 P2 12 34 44 2 P3 17 37 35 2 P8 45 42 21 3 P6 33 0 6 3 P2 7 6 42 3 P8 41 8 8 3 P6 32 16 28 3 P5 28 21 32 3 P4 20 29 41 3 P8 44 32 22 3 P4 23 35 42 4 P6 31 1 44 4 P4 18 5 6 4 P6 34 8 10 4 P1 2 10 20 4 P8 42 16 29 4 P8 43 26 37 4 P1 5 32 40 4 P5 30 37 5 4 P1 6 40 21 5 P2 10 0 6 5 P5 27 10 10 5 P4 19 20 34 5 P3 14 29 25 5 P1 3 35 27 5 P2 13 38 2 6 P7 38 0 16 6 P3 16 2 42 6 P5 26 6 16 6 P4 22 13 26 6 P1 1 22 32 6 P5 29 30 35 6 P7 40 37 44 | Makespan = 44 Ws1: Total_Time=43.0, Utilization=0.9773 Ws2: Total_Time=42.0, Utilization=0.9545 Ws3: Total_Time=42.0, Utilization=0.9545 Ws4: Total_Time=43.0, Utilization=0.9773 Ws5: Total_Time=41.0, Utilization=0.9318 Ws6: Total_Time=39.0, Utilization=0.8864 Average System Utilization: 0.9470 |
Makespan = 44 Run-time = 3144 seconds
Gantt Chart

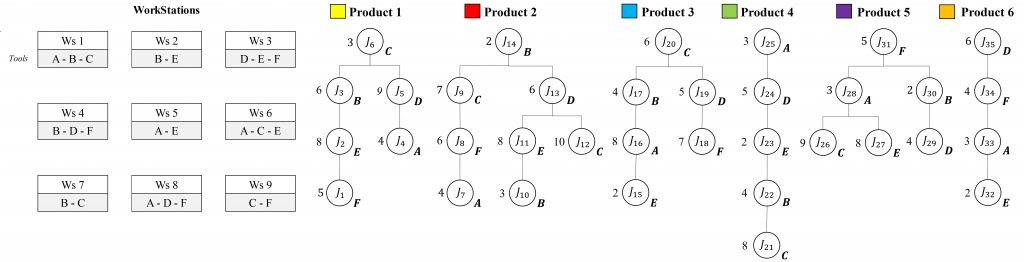
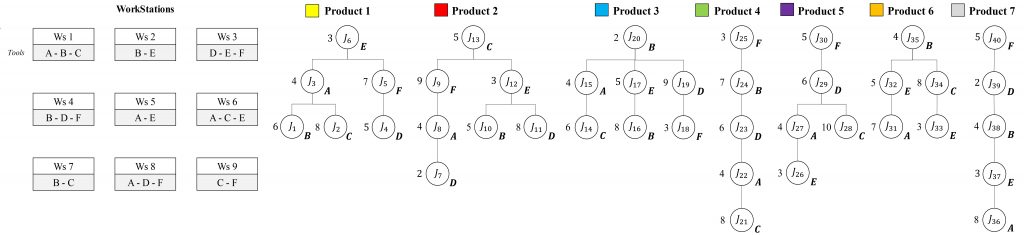
Matrix-Structure 3 x 3
Int_11
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 1 7 1000 1000 1000 7 1000 1000 1000 7 2 8 1000 1000 8 1000 1000 1000 8 1000 3 1000 6 1000 1000 1000 6 1000 1000 6 4 1000 1000 4 1000 4 1000 1000 4 1000 5 1000 1000 5 1000 1000 5 5 1000 1000 6 1000 3 1000 3 1000 1000 3 1000 1000 7 4 1000 1000 4 1000 1000 1000 4 1000 8 8 1000 1000 1000 8 1000 1000 1000 8 9 1000 1000 9 1000 1000 9 9 1000 1000 10 1000 1000 3 1000 3 1000 1000 3 1000 11 1000 6 1000 6 1000 1000 6 1000 1000 12 1000 5 1000 1000 1000 5 1000 1000 5 13 10 1000 1000 10 1000 1000 1000 10 1000 14 8 1000 1000 1000 8 1000 1000 1000 8 15 1000 1000 7 1000 7 1000 1000 7 1000 16 1000 6 1000 6 1000 1000 6 1000 1000 17 2 1000 1000 1000 2 1000 1000 1000 2 18 1000 1000 5 1000 5 1000 1000 5 1000 19 1000 1000 3 1000 1000 3 3 1000 1000 20 1000 6 1000 6 1000 1000 6 1000 1000 21 1000 4 1000 1000 1000 4 1000 1000 4 22 3 1000 1000 1000 3 1000 1000 1000 3 23 1000 1000 6 1000 1000 6 6 1000 1000 24 8 1000 1000 8 1000 1000 1000 8 1000 25 1000 5 1000 1000 1000 5 1000 1000 5 26 1000 4 1000 4 1000 1000 4 1000 1000 27 1000 1000 8 1000 1000 8 8 1000 1000 28 2 1000 1000 2 1000 1000 1000 2 1000 29 1000 1000 4 1000 4 1000 1000 4 1000 30 1000 3 1000 1000 1000 3 1000 1000 3 | Predecessor Successor 1 2 2 3 4 5 3 6 5 6 7 8 9 11 10 11 8 12 11 12 13 16 14 16 15 16 17 18 18 19 19 20 20 21 22 23 24 25 23 26 25 26 27 28 28 29 29 30 | WorkStation Product Task Start_Time Completion_Time 1 P5 24 0 7 1 P3 13 8 15 2 P5 25 8 21 2 P4 20 14 11 2 P4 21 20 21 3 P2 10 2 24 3 P3 15 5 7 3 P6 29 12 19 3 P1 5 16 11 4 P6 28 9 5 4 P2 11 11 17 4 P5 26 17 24 4 P1 6 21 18 5 P4 17 0 18 5 P4 18 2 12 5 P1 4 7 24 5 P2 8 11 2 6 P6 27 1 7 6 P4 19 11 14 6 P1 3 15 20 6 P6 30 21 24 7 P2 9 2 10 7 P5 23 11 17 7 P3 16 18 8 8 P2 7 3 13 8 P1 2 7 21 9 P1 1 0 9 9 P5 22 7 11 9 P3 14 10 16 9 P2 12 19 24 | Makespan = 24 Ws1: Total_Time=18.0, Utilization=0.7500 Ws2: Total_Time=15.0, Utilization=0.6250 Ws3: Total_Time=19.0, Utilization=0.7917 Ws4: Total_Time=15.0, Utilization=0.6250 Ws5: Total_Time=19.0, Utilization=0.7917 Ws6: Total_Time=20.0, Utilization=0.8333 Ws7: Total_Time=21.0, Utilization=0.8750 Ws8: Total_Time=12.0, Utilization=0.5000 Ws9: Total_Time=23.0, Utilization=0.9583 Average System Utilization: 0.7500 |
Makespan = 24 Run-time = 5,47 seconds
Gantt Chart

Int_12
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 1 1000 1000 5 5 1000 1000 1000 5 5 2 1000 8 8 1000 8 8 1000 1000 1000 3 6 6 1000 6 1000 1000 6 1000 1000 4 4 1000 1000 1000 4 4 4 1000 1000 5 1000 1000 9 9 1000 1000 1000 9 1000 6 3 1000 1000 1000 1000 3 3 1000 3 7 4 1000 1000 1000 4 4 4 1000 1000 8 1000 1000 6 6 1000 1000 1000 6 6 9 7 1000 1000 1000 1000 7 7 1000 7 10 3 3 1000 3 1000 1000 3 1000 1000 11 1000 8 8 1000 8 8 1000 1000 1000 12 10 1000 1000 1000 1000 10 10 1000 10 13 1000 1000 6 6 1000 1000 1000 6 1000 14 2 2 1000 2 1000 1000 2 1000 1000 15 1000 2 2 1000 2 2 1000 1000 1000 16 8 1000 1000 1000 8 8 8 1000 1000 17 4 4 1000 4 1000 1000 4 1000 1000 18 1000 1000 7 7 1000 1000 1000 7 7 19 1000 1000 5 5 1000 1000 1000 5 1000 20 3 1000 1000 1000 1000 3 3 1000 3 21 8 1000 1000 1000 1000 8 8 1000 8 22 4 4 1000 4 1000 1000 4 1000 1000 23 1000 2 2 1000 2 2 1000 1000 1000 24 1000 1000 5 5 1000 1000 1000 5 1000 25 3 1000 1000 1000 3 3 3 1000 1000 26 9 1000 1000 1000 1000 9 9 1000 9 27 1000 8 8 1000 8 8 1000 1000 1000 28 3 1000 1000 1000 3 3 3 1000 1000 29 1000 1000 4 4 1000 1000 1000 4 1000 30 2 2 1000 2 1000 1000 2 1000 1000 31 1000 1000 5 5 1000 1000 1000 5 5 32 1000 2 2 1000 2 2 1000 1000 1000 33 3 1000 1000 1000 3 3 3 1000 1000 34 1000 1000 4 4 1000 1000 1000 4 4 35 1000 1000 2 2 1000 1000 1000 2 1000 | Predecessor Successor 1 2 2 3 4 5 3 6 5 6 7 8 8 9 10 11 11 13 12 13 9 14 13 14 15 16 16 17 18 19 17 20 19 20 21 22 22 23 23 24 24 25 26 28 27 28 29 30 28 31 30 31 32 33 33 34 34 35 | WorkStation Product Task Start_Time Completion_Time 1 P4 21 0 5 1 P4 22 8 13 1 P2 9 13 19 1 P2 14 20 4 2 P3 15 0 16 2 P1 2 5 22 2 P1 3 13 7 3 P5 27 1 13 3 P3 19 9 20 3 P2 13 14 3 4 P5 29 1 12 4 P5 30 5 10 4 P2 8 7 20 4 P4 24 14 22 4 P6 35 19 2 5 P1 4 0 15 5 P2 11 4 19 5 P4 23 12 7 5 P5 28 14 14 5 P4 25 19 22 6 P2 12 0 8 6 P6 32 10 12 6 P6 33 12 14 6 P1 6 19 19 7 P2 10 0 22 7 P2 7 3 14 7 P3 16 7 9 7 P3 17 15 17 8 P3 18 0 5 8 P1 5 7 7 8 P5 31 17 22 9 P1 1 0 12 9 P5 26 5 15 9 P6 34 15 19 9 P3 20 19 21 | Makespan = 22 Ws1: Total_Time=21.0, Utilization=0.9545 Ws2: Total_Time=16.0, Utilization=0.7273 Ws3: Total_Time=19.0, Utilization=0.8636 Ws4: Total_Time=19.0, Utilization=0.8636 Ws5: Total_Time=20.0, Utilization=0.9091 Ws6: Total_Time=18.0, Utilization=0.8182 Ws7: Total_Time=19.0, Utilization=0.8636 Ws8: Total_Time=21.0, Utilization=0.9545 Ws9: Total_Time=21.0, Utilization=0.9545 Average System Utilization: 0.8788 |
Makespan = 22 Run-time = 57,7seconds
Gantt Chart

Int_13
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 1 6 6 1000 6 1000 1000 6 1000 1000 2 8 1000 1000 1000 1000 8 8 1000 8 3 4 1000 1000 1000 4 4 4 1000 1000 4 1000 1000 5 5 1000 1000 1000 5 1000 5 1000 1000 7 7 1000 1000 1000 7 7 6 1000 3 3 1000 3 3 1000 1000 1000 7 1000 1000 2 2 1000 1000 1000 2 1000 8 4 1000 1000 1000 4 4 4 1000 1000 9 1000 1000 9 9 1000 1000 1000 9 9 10 5 5 1000 5 1000 1000 5 1000 1000 11 1000 1000 8 8 1000 1000 1000 8 1000 12 1000 3 3 1000 3 3 1000 1000 1000 13 5 1000 1000 1000 1000 5 5 1000 5 14 6 1000 1000 1000 1000 6 6 1000 6 15 4 1000 1000 1000 4 4 4 1000 1000 16 8 8 1000 8 1000 1000 8 1000 1000 17 1000 5 5 1000 5 5 1000 1000 1000 18 1000 1000 3 3 1000 1000 1000 3 3 19 1000 1000 9 9 1000 1000 1000 9 1000 20 2 2 1000 2 1000 1000 2 1000 1000 21 8 1000 1000 1000 1000 8 8 1000 8 22 4 1000 1000 1000 4 4 4 1000 1000 23 1000 1000 6 6 1000 1000 1000 6 1000 24 7 7 1000 7 1000 1000 7 1000 1000 25 1000 1000 3 3 1000 1000 1000 3 3 26 1000 3 3 1000 3 3 1000 1000 1000 27 4 1000 1000 1000 4 4 4 1000 1000 28 10 1000 1000 1000 1000 10 10 1000 10 29 1000 1000 6 6 1000 1000 1000 6 1000 30 1000 1000 5 5 1000 1000 1000 5 5 31 7 1000 1000 1000 7 7 7 1000 1000 32 1000 5 5 1000 5 5 1000 1000 1000 33 1000 3 3 1000 3 3 1000 1000 1000 34 8 1000 1000 1000 1000 8 8 1000 8 35 4 4 1000 4 1000 1000 4 1000 1000 36 8 1000 1000 1000 8 8 8 1000 1000 37 1000 3 3 1000 3 3 1000 1000 1000 38 4 4 1000 4 1000 1000 4 1000 1000 39 1000 1000 2 2 1000 1000 1000 2 1000 40 1000 1000 5 5 1000 1000 1000 5 5 | Predecessor Successor 1 3 2 3 4 5 3 6 5 6 7 8 8 9 10 12 11 12 9 13 12 13 14 15 16 17 18 19 15 20 17 20 19 20 21 22 22 23 23 24 24 25 26 27 27 29 28 29 29 30 31 32 33 34 32 35 34 35 36 37 37 38 38 39 39 40 | WorkStation Product Task Start_Time Completion_Time 1 P3 14 2 19 1 P4 22 8 18 1 P3 15 12 24 1 P7 38 16 8 1 P1 3 20 17 1 P3 20 26 27 2 P3 16 2 10 2 P7 37 10 14 2 P1 1 13 23 2 P6 32 19 5 2 P6 35 24 8 3 P3 18 0 17 3 P1 4 3 28 3 P2 7 8 8 3 P1 5 10 16 3 P5 29 17 10 4 P2 10 0 22 4 P3 19 5 3 4 P2 9 14 14 4 P4 25 25 28 5 P7 36 0 8 5 P6 33 10 12 5 P5 27 13 18 5 P1 6 24 25 6 P6 31 0 28 6 P5 26 7 10 6 P2 8 10 17 6 P2 12 14 10 6 P3 17 17 23 6 P2 13 23 28 7 P4 21 0 7 7 P1 2 10 24 7 P4 24 18 13 8 P2 11 0 23 8 P4 23 12 28 8 P7 39 20 8 8 P5 30 23 13 9 P5 28 0 20 9 P6 34 15 22 9 P7 40 23 28 | Makespan = 28 Ws1: Total_Time=24.0, Utilization=0.8571 Ws2: Total_Time=26.0, Utilization=0.9286 Ws3: Total_Time=23.0, Utilization=0.8214 Ws4: Total_Time=26.0, Utilization=0.9286 Ws5: Total_Time=18.0, Utilization=0.6429 Ws6: Total_Time=27.0, Utilization=0.9643 Ws7: Total_Time=23.0, Utilization=0.8214 Ws8: Total_Time=21.0, Utilization=0.7500 Ws9: Total_Time=23.0, Utilization=0.8214 Average System Utilization: 0.8373 |
Makespan = 28 Run-time = 392 seconds
Gantt Chart

Int_14
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 1 6 1000 1000 1000 6 6 6 1000 1000 2 4 1000 1000 1000 1000 4 4 1000 4 3 7 7 1000 7 1000 1000 7 1000 1000 4 1000 1000 5 5 1000 1000 1000 5 1000 5 1000 3 3 1000 3 3 1000 1000 1000 6 1000 1000 8 8 1000 1000 1000 8 8 7 2 2 1000 2 1000 1000 2 1000 1000 8 9 1000 1000 1000 1000 9 9 1000 9 9 1000 1000 4 4 1000 1000 1000 4 1000 10 5 1000 1000 1000 5 5 5 1000 1000 11 1000 1000 10 10 1000 1000 1000 10 10 12 1000 6 6 1000 6 6 1000 1000 1000 13 4 1000 1000 1000 1000 4 4 1000 4 14 3 3 1000 3 1000 1000 3 1000 1000 15 6 1000 1000 1000 6 6 6 1000 1000 16 1000 1000 2 2 1000 1000 1000 2 1000 17 1000 8 8 1000 8 8 1000 1000 1000 18 1000 1000 3 3 1000 1000 1000 3 3 19 1000 6 6 1000 6 6 1000 1000 1000 20 8 1000 1000 1000 8 8 8 1000 1000 21 1000 1000 9 9 1000 1000 1000 9 1000 22 3 1000 1000 1000 1000 3 3 1000 3 23 10 10 1000 10 1000 1000 10 1000 1000 24 1000 1000 4 4 1000 1000 1000 4 4 25 1000 1000 2 2 1000 1000 1000 2 1000 26 1000 4 4 1000 4 4 1000 1000 1000 27 8 8 1000 8 1000 1000 8 1000 1000 28 2 1000 1000 1000 2 2 2 1000 1000 29 1000 1000 6 6 1000 1000 1000 6 6 30 1000 1000 7 7 1000 1000 1000 7 1000 31 5 1000 1000 1000 1000 5 5 1000 5 32 1000 1000 3 3 1000 1000 1000 3 3 33 10 1000 1000 1000 1000 10 10 1000 10 34 1000 4 4 1000 4 4 1000 1000 1000 35 2 1000 1000 1000 2 2 2 1000 1000 36 5 1000 1000 1000 1000 5 5 1000 5 37 1000 1000 9 9 1000 1000 1000 9 1000 38 4 1000 1000 1000 4 4 4 1000 1000 39 1000 7 7 1000 7 7 1000 1000 1000 40 6 6 1000 6 1000 1000 6 1000 1000 41 1000 1000 8 8 1000 1000 1000 8 8 42 5 1000 1000 1000 1000 5 5 1000 5 43 1000 1000 10 10 1000 1000 1000 10 1000 44 3 1000 1000 1000 3 3 3 1000 1000 45 4 4 1000 4 1000 1000 4 1000 1000 | Predecessor Successor 1 2 3 4 2 5 4 5 6 7 7 8 5 9 8 9 10 12 11 12 13 14 15 16 14 17 16 17 12 18 17 18 19 20 21 22 23 24 20 25 22 25 24 25 26 27 27 28 28 29 29 30 30 31 32 33 33 34 34 35 36 38 37 38 38 40 39 40 41 42 43 44 42 45 44 45 | WorkStation Product Task Start_Time Completion_Time 1 P2 14 6 12 1 P1 7 9 25 1 P5 33 11 12 1 P1 2 21 25 1 P6 40 26 28 2 P4 27 4 8 2 P2 17 13 11 2 P5 34 21 21 2 P1 5 25 32 2 P7 45 28 19 3 P7 41 0 23 3 P2 16 10 29 3 P2 11 13 4 3 P3 24 24 9 3 P1 9 28 10 4 P7 43 0 12 4 P3 23 10 21 4 P4 30 20 32 4 P3 25 30 16 5 P4 26 0 30 5 P1 1 6 18 5 P4 28 12 28 5 P2 10 14 20 5 P7 44 19 28 5 P3 20 22 32 6 P2 13 0 4 6 P2 15 4 12 6 P3 19 10 14 6 P6 39 16 20 6 P2 12 23 27 7 P6 36 0 32 7 P1 3 5 11 7 P1 8 12 21 7 P6 38 21 25 7 P3 22 25 32 7 P5 35 30 5 8 P6 37 0 9 8 P3 21 9 25 8 P1 4 20 23 8 P2 18 29 32 9 P1 6 0 8 9 P5 32 8 25 9 P4 29 14 10 9 P7 42 20 22 9 P4 31 27 32 | Makespan = 32 Ws1: Total_Time=25.0, Utilization=0.7812 Ws2: Total_Time=27.0, Utilization=0.8438 Ws3: Total_Time=28.0, Utilization=0.8750 Ws4: Total_Time=29.0, Utilization=0.9062 Ws5: Total_Time=28.0, Utilization=0.8750 Ws6: Total_Time=29.0, Utilization=0.9062 Ws7: Total_Time=30.0, Utilization=0.9375 Ws8: Total_Time=26.0, Utilization=0.8125 Ws9: Total_Time=27.0, Utilization=0.8438 Average System Utilization: 0.8646 |
Makespan = 32 Run-time = 948 seconds
Gantt Chart

Int_15
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 1 2 1000 1000 1000 2 2 2 1000 1000 2 5 5 1000 5 1000 1000 5 1000 1000 3 1000 1000 6 6 1000 1000 1000 6 1000 4 4 1000 1000 1000 1000 4 4 1000 4 5 1000 7 7 1000 7 7 1000 1000 1000 6 1000 1000 3 3 1000 1000 1000 3 3 7 9 1000 1000 1000 9 9 9 1000 1000 8 1000 4 4 1000 4 4 1000 1000 1000 9 1000 1000 5 5 1000 1000 1000 5 1000 10 6 6 1000 6 1000 1000 6 1000 1000 11 8 1000 1000 1000 1000 8 8 1000 8 12 1000 1000 4 4 1000 1000 1000 4 4 13 1000 7 7 1000 7 7 1000 1000 1000 14 5 5 1000 5 1000 1000 5 1000 1000 15 1000 1000 3 3 1000 1000 1000 3 1000 16 9 1000 1000 1000 9 9 9 1000 1000 17 2 1000 1000 1000 1000 2 2 1000 2 18 4 1000 1000 1000 4 4 4 1000 1000 19 1000 1000 5 5 1000 1000 1000 5 1000 20 3 3 1000 3 1000 1000 3 1000 1000 21 1000 9 9 1000 9 9 1000 1000 1000 22 6 1000 1000 1000 1000 6 6 1000 6 23 10 10 1000 10 1000 1000 10 1000 1000 24 2 1000 1000 1000 2 2 2 1000 1000 25 1000 1000 6 6 1000 1000 1000 6 6 26 6 1000 1000 1000 6 6 6 1000 1000 27 8 1000 1000 1000 1000 8 8 1000 8 28 1000 4 4 1000 4 4 1000 1000 1000 29 1000 1000 6 6 1000 1000 1000 6 1000 30 1000 1000 5 5 1000 1000 1000 5 5 31 7 7 1000 7 1000 1000 7 1000 1000 32 8 1000 1000 1000 1000 8 8 1000 8 33 1000 1000 10 10 1000 1000 1000 10 1000 34 1000 1000 6 6 1000 1000 1000 6 6 35 1000 3 3 1000 3 3 1000 1000 1000 36 4 1000 1000 1000 4 4 4 1000 1000 37 10 10 1000 10 1000 1000 10 1000 1000 38 1000 2 2 1000 2 2 1000 1000 1000 39 4 1000 1000 1000 4 4 4 1000 1000 40 1000 1000 8 8 1000 1000 1000 8 8 41 3 1000 1000 1000 1000 3 3 1000 3 42 1000 1000 6 6 1000 1000 1000 6 1000 43 9 1000 1000 1000 1000 9 9 1000 9 44 1000 1000 5 5 1000 1000 1000 5 5 45 10 1000 1000 1000 10 10 10 1000 1000 46 4 4 1000 4 1000 1000 4 1000 1000 47 1000 3 3 1000 3 3 1000 1000 1000 48 8 1000 1000 1000 1000 8 8 1000 8 49 4 1000 1000 1000 4 4 4 1000 1000 50 2 1000 1000 1000 1000 2 2 1000 2 | Predecessor Successor 1 2 3 4 2 5 4 5 6 8 7 8 5 9 8 9 10 12 11 12 13 16 14 16 15 16 12 17 16 17 18 19 19 20 21 22 23 24 20 25 22 25 24 25 26 27 27 28 28 29 29 30 30 31 32 33 33 34 34 35 35 36 37 39 38 39 40 41 39 42 41 42 43 44 45 46 44 47 46 47 48 50 49 50 | WorkStation Product Task Start_Time Completion_Time 1 P1 1 0 2 1 P8 49 2 11 1 P4 27 6 6 1 P6 37 14 21 1 P3 20 24 31 1 P3 24 28 3 1 P2 17 34 9 2 P2 13 1 16 2 P2 10 8 36 2 P4 28 14 14 2 P7 46 22 8 2 P7 47 26 34 2 P4 31 29 8 3 P1 6 0 14 3 P3 21 3 3 3 P1 8 12 31 3 P6 38 16 36 3 P4 29 18 12 3 P1 9 31 24 4 P2 15 0 27 4 P1 2 6 12 4 P3 23 11 30 4 P7 44 21 21 4 P3 25 30 30 5 P4 26 0 36 5 P3 18 8 6 5 P7 45 12 14 5 P6 39 24 18 5 P5 35 28 24 6 P2 11 0 29 6 P7 43 8 36 6 P1 4 17 8 6 P6 41 21 18 6 P1 5 24 24 6 P8 50 34 31 7 P1 7 0 36 7 P2 14 9 24 7 P8 48 14 18 7 P2 16 22 28 7 P5 36 32 18 8 P1 3 0 24 8 P5 33 8 36 8 P3 19 19 17 8 P4 30 24 26 8 P6 42 30 22 9 P5 32 0 26 9 P6 40 10 29 9 P5 34 18 22 9 P3 22 24 6 9 P2 12 30 36 | Makespan = 36 Ws1: Total_Time=31.0, Utilization=0.8611 Ws2: Total_Time=31.0, Utilization=0.8611 Ws3: Total_Time=29.0, Utilization=0.8056 Ws4: Total_Time=29.0, Utilization=0.8056 Ws5: Total_Time=27.0, Utilization=0.7500 Ws6: Total_Time=33.0, Utilization=0.9167 Ws7: Total_Time=35.0, Utilization=0.9722 Ws8: Total_Time=32.0, Utilization=0.8889 Ws9: Total_Time=32.0, Utilization=0.8889 Average System Utilization: 0.8611 |
Makespan = 36 Run-time = 507 seconds
Gantt Chart

Int_16
| Input Data: Processing Time | List of Precedents: | Output Data: | Utilization Rate: |
|---|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 1 1000 6 6 1000 6 6 1000 1000 1000 2 2 2 1000 2 1000 1000 2 1000 1000 3 8 1000 1000 1000 1000 8 8 1000 8 4 4 1000 1000 1000 4 4 4 1000 1000 5 1000 1000 9 9 1000 1000 1000 9 9 6 1000 1000 7 7 1000 1000 1000 7 1000 7 3 1000 1000 1000 1000 3 3 1000 3 8 5 5 1000 5 1000 1000 5 1000 1000 9 1000 4 4 1000 4 4 1000 1000 1000 10 1000 1000 2 2 1000 1000 1000 2 1000 11 1000 1000 3 3 1000 1000 1000 3 3 12 7 1000 1000 1000 7 7 7 1000 1000 13 1000 5 5 1000 5 5 1000 1000 1000 14 10 1000 1000 1000 1000 10 10 1000 10 15 8 8 1000 8 1000 1000 8 1000 1000 16 1000 1000 4 4 1000 1000 1000 4 1000 17 6 1000 1000 1000 1000 6 6 1000 6 18 1000 9 9 1000 9 9 1000 1000 1000 19 1000 1000 3 3 1000 1000 1000 3 1000 20 2 1000 1000 1000 1000 2 2 1000 2 21 5 5 1000 5 1000 1000 5 1000 1000 22 6 1000 1000 1000 6 6 6 1000 1000 23 1000 1000 8 8 1000 1000 1000 8 8 24 4 1000 1000 1000 4 4 4 1000 1000 25 1000 1000 10 10 1000 1000 1000 10 10 26 2 1000 1000 1000 1000 2 2 1000 2 27 1000 4 4 1000 4 4 1000 1000 1000 28 1000 1000 6 6 1000 1000 1000 6 1000 29 5 5 1000 5 1000 1000 5 1000 1000 30 8 1000 1000 1000 8 8 8 1000 1000 31 3 1000 1000 1000 1000 3 3 1000 3 32 1000 9 9 1000 9 9 1000 1000 1000 33 1000 1000 6 6 1000 1000 1000 6 1000 34 1000 1000 7 7 1000 1000 1000 7 7 35 9 1000 1000 1000 1000 9 9 1000 9 36 3 1000 1000 1000 3 3 3 1000 1000 37 1000 1000 8 8 1000 1000 1000 8 1000 38 1000 2 2 1000 2 2 1000 1000 1000 39 4 4 1000 4 1000 1000 4 1000 1000 40 1000 1000 5 5 1000 1000 1000 5 5 41 1000 1000 4 4 1000 1000 1000 4 1000 42 1000 6 6 1000 6 6 1000 1000 1000 43 7 7 1000 7 1000 1000 7 1000 1000 44 2 1000 1000 1000 1000 2 2 1000 2 45 3 1000 1000 1000 3 3 3 1000 1000 46 1000 1000 9 9 1000 1000 1000 9 9 47 1000 5 5 1000 5 5 1000 1000 1000 48 10 1000 1000 1000 10 10 10 1000 1000 49 1000 1000 5 5 1000 1000 1000 5 1000 50 6 6 1000 6 1000 1000 6 1000 1000 51 4 1000 1000 1000 1000 4 4 1000 4 52 1000 1000 2 2 1000 1000 1000 2 1000 53 5 1000 1000 1000 5 5 5 1000 1000 54 6 6 1000 6 1000 1000 6 1000 1000 55 1000 3 3 1000 3 3 1000 1000 1000 | Predecessor Successor 1 2 3 4 2 5 4 5 6 7 7 8 5 9 8 9 10 12 11 12 13 16 14 16 15 16 12 17 16 17 18 19 20 21 22 23 19 24 21 24 23 24 25 26 26 27 27 28 28 29 30 31 31 33 32 33 34 36 35 36 37 39 38 39 36 40 39 40 41 42 43 44 42 45 44 45 46 47 47 48 48 49 49 50 50 51 52 53 53 54 54 55 | WorkStation Product Task Start_Time Completion_Time 1 P3 20 0 15 1 P9 53 2 17 1 P4 26 11 25 1 P7 44 13 29 1 P1 2 15 38 1 P8 48 17 13 1 P1 7 28 31 2 P7 43 0 36 2 P2 13 7 42 2 P5 32 12 21 2 P6 38 21 19 2 P3 21 27 36 2 P8 50 32 12 3 P8 46 0 20 3 P6 37 9 8 3 P4 27 17 36 3 P4 28 21 42 3 P6 40 27 9 3 P5 33 33 12 3 P9 55 39 2 4 P2 15 0 32 4 P3 19 9 28 4 P7 41 12 36 4 P2 11 16 40 4 P2 10 19 11 4 P9 54 21 13 4 P8 49 27 21 4 P2 16 32 27 4 P4 29 37 42 5 P5 30 0 8 5 P1 1 9 17 5 P7 42 16 21 5 P1 4 25 39 5 P1 9 38 20 6 P3 18 0 10 6 P8 47 9 23 6 P3 22 22 17 6 P2 12 29 23 6 P2 17 36 27 7 P6 35 1 32 7 P2 14 10 16 7 P4 26 11 22 7 P4 29 37 7 7 P7 45 28 15 7 P1 8 31 31 7 P3 24 36 9 8 P9 52 0 14 8 P1 6 6 27 8 P6 34 13 32 8 P1 5 29 38 9 P4 25 1 42 9 P5 31 14 2 9 P1 3 17 7 9 P3 23 28 27 9 P8 51 38 42 | Makespan = 42 Ws1: Total_Time=26.0, Utilization=0.6190 Ws2: Total_Time=34.0, Utilization=0.8095 Ws3: Total_Time=41.0, Utilization=0.9762 Ws4: Total_Time=40.0, Utilization=0.9524 Ws5: Total_Time=28.0, Utilization=0.6667 Ws6: Total_Time=33.0, Utilization=0.7857 Ws7: Total_Time=38.0, Utilization=0.9048 Ws8: Total_Time=25.0, Utilization=0.5952 Ws9: Total_Time=33.0, Utilization=0.7857 Average System Utilization: 0.7884 |
Makespan = 42 Run-time = 2278 seconds
Gantt Chart

Matrix-Structure 3 x 4
Int_17
| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 1 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 2 1000 4 1000 1000 4 1000 1000 1000 4 1000 4 1000 3 8 1000 1000 1000 1000 8 1000 1000 8 1000 1000 8 4 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 1000 5 1000 7 1000 1000 7 1000 7 1000 1000 7 1000 1000 6 1000 1000 2 2 1000 1000 2 1000 1000 1000 1000 2 7 1000 1000 9 9 1000 1000 1000 1000 9 1000 9 1000 8 2 1000 1000 1000 1000 2 2 1000 1000 1000 2 1000 9 1000 8 1000 1000 8 1000 8 1000 1000 8 1000 1000 10 1000 7 1000 1000 7 1000 1000 1000 7 1000 7 1000 11 6 1000 1000 1000 6 1000 1000 6 1000 6 1000 1000 12 1000 1000 4 4 1000 1000 4 1000 1000 1000 1000 4 13 1000 1000 10 10 1000 1000 1000 10 1000 1000 1000 10 14 5 1000 1000 1000 1000 5 1000 1000 5 1000 1000 5 15 1000 1000 3 3 1000 1000 1000 1000 3 1000 3 1000 16 1000 9 1000 1000 9 1000 9 1000 1000 9 1000 1000 17 4 1000 1000 1000 1000 4 1000 1000 4 1000 1000 4 18 1000 1000 2 2 1000 1000 2 1000 1000 1000 1000 2 19 7 1000 1000 1000 1000 7 7 1000 1000 1000 7 1000 20 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 1000 21 1000 1000 5 5 1000 1000 1000 5 1000 1000 1000 5 22 1000 8 1000 1000 8 1000 1000 1000 8 1000 8 1000 23 1000 1000 6 6 1000 1000 1000 1000 6 1000 6 1000 24 4 1000 1000 1000 1000 4 4 1000 1000 1000 4 1000 25 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 26 7 1000 1000 1000 7 1000 1000 7 1000 7 1000 1000 27 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 28 4 1000 1000 1000 1000 4 1000 1000 4 1000 1000 4 29 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 30 1000 1000 6 6 1000 1000 6 1000 1000 1000 1000 6 31 1000 5 1000 1000 5 1000 1000 1000 5 1000 5 1000 32 1000 1000 2 2 1000 1000 1000 1000 2 1000 2 1000 33 1000 1000 8 8 1000 1000 1000 8 1000 1000 1000 8 34 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 35 2 1000 1000 1000 2 1000 1000 2 1000 2 1000 1000 36 1000 1000 8 8 1000 1000 8 1000 1000 1000 1000 8 37 1000 1000 4 4 1000 1000 1000 1000 4 1000 4 1000 38 1000 1000 10 10 1000 1000 1000 10 1000 1000 1000 10 39 1000 7 1000 1000 7 1000 7 1000 1000 7 1000 1000 40 6 1000 1000 1000 1000 6 1000 1000 6 1000 1000 6 | Predecessor Successor 1 2 2 3 4 5 3 6 5 6 7 8 8 9 10 11 12 13 11 14 13 14 9 15 14 15 16 17 18 19 20 21 17 22 19 22 21 22 23 24 24 25 25 26 26 27 28 29 29 31 30 31 31 32 33 34 32 35 34 35 36 37 38 39 37 40 39 40 | WorkStation Product Task Start_Time Completion_Time 1 P1 4 0 6 1 P2 8 10 13 1 P1 3 13 21 2 P2 10 0 10 2 P5 29 7 21 2 P4 25 10 23 2 P2 9 12 9 3 P6 38 0 12 3 P3 21 10 20 3 P1 6 21 7 4 P2 12 0 15 4 P2 13 4 4 4 P2 15 20 14 5 P3 16 0 20 5 P2 11 9 23 5 P3 22 15 9 6 P5 28 2 14 6 P4 24 6 2 6 P5 34 10 13 6 P6 40 17 10 7 P1 1 0 15 7 P5 30 8 23 7 P1 5 14 6 8 P5 33 0 10 8 P4 26 12 12 8 P4 27 19 19 9 P2 7 0 22 9 P1 2 9 6 9 P6 37 13 10 9 P5 32 19 14 10 P3 20 0 19 10 P6 39 10 21 10 P5 35 21 8 11 P4 23 0 16 11 P3 19 6 23 11 P5 31 14 10 12 P3 18 0 17 12 P6 36 2 10 12 P3 17 10 17 12 P2 14 15 23 |
| Utilization Rate: |
|---|
| Makespan = 23 Ws1: Total_Time=20.0, Utilization=0.8696 Ws2: Total_Time=20.0, Utilization=0.8696 Ws3: Total_Time=17.0, Utilization=0.7391 Ws4: Total_Time=17.0, Utilization=0.7391 Ws5: Total_Time=23.0, Utilization=1.0000 Ws6: Total_Time=20.0, Utilization=0.8696 Ws7: Total_Time=19.0, Utilization=0.8261 Ws8: Total_Time=18.0, Utilization=0.7826 Ws9: Total_Time=19.0, Utilization=0.8261 Ws10: Total_Time=19.0, Utilization=0.8261 Ws11: Total_Time=18.0, Utilization=0.7826 Ws12: Total_Time=19.0, Utilization=0.8261 Average System Utilization: 0.8297 |
Makespan = 23 Run-time = 32,8 seconds
Gantt Chart

Int_18
| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 1 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 2 1000 4 1000 1000 4 1000 1000 1000 4 1000 4 1000 3 1000 1000 10 10 1000 1000 1000 10 1000 1000 1000 10 4 8 1000 1000 1000 1000 8 1000 1000 8 1000 1000 8 5 1000 1000 3 3 1000 1000 1000 1000 3 1000 3 1000 6 5 1000 1000 1000 1000 5 5 1000 1000 1000 5 1000 7 6 1000 1000 1000 6 1000 1000 6 1000 6 1000 1000 8 1000 7 1000 1000 7 1000 7 1000 1000 7 1000 1000 9 1000 1000 5 5 1000 1000 5 1000 1000 1000 1000 5 10 7 1000 1000 1000 1000 7 7 1000 1000 1000 7 1000 11 1000 1000 9 9 1000 1000 1000 1000 9 1000 9 1000 12 1000 8 1000 1000 8 1000 8 1000 1000 8 1000 1000 13 1000 4 1000 1000 4 1000 1000 1000 4 1000 4 1000 14 6 1000 1000 1000 6 1000 1000 6 1000 6 1000 1000 15 1000 1000 10 10 1000 1000 10 1000 1000 1000 1000 10 16 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 17 5 1000 1000 1000 1000 5 1000 1000 5 1000 1000 5 18 1000 1000 3 3 1000 1000 1000 1000 3 1000 3 1000 19 1000 1000 8 8 1000 1000 1000 1000 8 1000 8 1000 20 1000 5 1000 1000 5 1000 5 1000 1000 5 1000 1000 21 4 1000 1000 1000 1000 4 1000 1000 4 1000 1000 4 22 1000 1000 2 2 1000 1000 2 1000 1000 1000 1000 2 23 7 1000 1000 1000 1000 7 7 1000 1000 1000 7 1000 24 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 1000 25 1000 1000 5 5 1000 1000 1000 5 1000 1000 1000 5 26 1000 6 1000 1000 6 1000 1000 1000 6 1000 6 1000 27 8 1000 1000 1000 8 1000 1000 8 1000 8 1000 1000 28 4 1000 1000 1000 1000 4 4 1000 1000 1000 4 1000 29 1000 5 1000 1000 5 1000 5 1000 1000 5 1000 1000 30 1000 1000 7 7 1000 1000 7 1000 1000 1000 1000 7 31 1000 3 1000 1000 3 1000 1000 1000 3 1000 3 1000 32 1000 1000 6 6 1000 1000 1000 1000 6 1000 6 1000 33 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 34 4 1000 1000 1000 1000 4 1000 1000 4 1000 1000 4 35 1000 1000 8 8 1000 1000 8 1000 1000 1000 1000 8 36 1000 5 1000 1000 5 1000 1000 1000 5 1000 5 1000 37 1000 1000 4 4 1000 1000 1000 1000 4 1000 4 1000 38 1000 1000 9 9 1000 1000 1000 9 1000 1000 1000 9 39 7 1000 1000 1000 1000 7 7 1000 1000 1000 7 1000 40 2 1000 1000 1000 2 1000 1000 2 1000 2 1000 1000 41 1000 1000 8 8 1000 1000 8 1000 1000 1000 1000 8 42 1000 6 1000 1000 6 1000 1000 1000 6 1000 6 1000 43 1000 1000 10 10 1000 1000 1000 10 1000 1000 1000 10 44 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 45 4 1000 1000 1000 1000 4 1000 1000 4 1000 1000 4 | Predecessor Successor 1 2 2 4 3 4 5 6 6 7 7 8 4 9 8 9 10 12 11 12 13 14 15 16 14 17 16 17 12 18 17 18 19 20 20 21 22 23 24 25 21 26 23 26 25 26 27 28 28 29 29 30 30 31 32 33 34 35 33 36 35 36 38 39 37 40 39 40 41 42 42 43 43 44 44 45 | WorkStation Product Task Start_Time Completion_Time 1 P5 34 4 6 1 P4 28 8 12 1 P1 4 12 12 1 P3 21 20 20 1 P6 40 29 5 2 P1 2 8 12 2 P2 12 15 18 2 P3 26 24 25 3 P1 5 2 31 3 P5 32 5 7 3 P2 16 11 15 3 P3 22 14 23 3 P4 30 17 12 4 P6 38 0 23 4 P7 43 14 10 4 P6 37 24 14 4 P2 18 28 28 5 P4 27 0 31 5 P2 13 8 8 5 P3 20 12 17 5 P2 14 17 24 5 P5 36 26 16 6 P2 10 0 23 6 P1 6 7 12 6 P3 23 16 24 6 P2 17 23 30 7 P2 15 0 8 7 P5 33 11 12 7 P6 39 14 17 7 P7 44 24 24 8 P1 3 2 27 8 P1 7 12 11 9 P3 19 0 14 9 P7 42 8 8 9 P7 45 27 16 10 P3 24 2 31 10 P4 29 12 28 10 P1 8 18 9 11 P1 1 0 21 11 P2 11 6 31 11 P4 31 24 8 12 P7 41 0 14 12 P5 35 8 24 12 P3 25 19 27 12 P1 9 26 31 |
| Utilization Rate: |
|---|
| Makespan = 31 Ws1: Total_Time=22.0, Utilization=0.7097 Ws2: Total_Time=18.0, Utilization=0.5806 Ws3: Total_Time=21.0, Utilization=0.6774 Ws4: Total_Time=26.0, Utilization=0.8387 Ws5: Total_Time=28.0, Utilization=0.9032 Ws6: Total_Time=24.0, Utilization=0.7742 Ws7: Total_Time=23.0, Utilization=0.7419 Ws8: Total_Time=16.0, Utilization=0.5161 Ws9: Total_Time=18.0, Utilization=0.5806 Ws10: Total_Time=22.0, Utilization=0.7097 Ws11: Total_Time=18.0, Utilization=0.5806 Ws12: Total_Time=26.0, Utilization=0.8387 Average System Utilization: 0.7043 |
Makespan = 31 Run-time = 472 seconds
Gantt Chart

Int_19
| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 1 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 1000 2 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 3 5 1000 1000 1000 1000 5 5 1000 1000 1000 5 1000 4 6 1000 1000 1000 1000 6 1000 1000 6 1000 1000 6 5 1000 8 1000 1000 8 1000 1000 1000 8 1000 8 1000 6 1000 7 1000 1000 7 1000 7 1000 1000 7 1000 1000 7 2 1000 1000 1000 2 1000 1000 2 1000 2 1000 1000 8 1000 1000 9 9 1000 1000 1000 1000 9 1000 9 1000 9 1000 1000 4 4 1000 1000 4 1000 1000 1000 1000 4 10 1000 1000 5 5 1000 1000 5 1000 1000 1000 1000 5 11 1000 10 1000 1000 10 1000 1000 1000 10 1000 10 1000 12 8 1000 1000 1000 8 1000 1000 8 1000 8 1000 1000 13 7 1000 1000 1000 7 1000 1000 7 1000 7 1000 1000 14 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 15 1000 1000 9 9 1000 1000 1000 1000 9 1000 9 1000 16 3 1000 1000 1000 1000 3 1000 1000 3 1000 1000 3 17 2 1000 1000 1000 1000 2 2 1000 1000 1000 2 1000 18 1000 1000 5 5 1000 1000 5 1000 1000 1000 1000 5 19 2 1000 1000 1000 2 1000 1000 2 1000 2 1000 1000 20 1000 1000 5 5 1000 1000 1000 5 1000 1000 1000 5 21 1000 4 1000 1000 4 1000 4 1000 1000 4 1000 1000 22 9 1000 1000 1000 1000 9 1000 1000 9 1000 1000 9 23 1000 1000 3 3 1000 1000 1000 1000 3 1000 3 1000 24 1000 6 1000 1000 6 1000 1000 1000 6 1000 6 1000 25 1000 9 1000 1000 9 1000 1000 1000 9 1000 9 1000 26 1000 1000 4 4 1000 1000 1000 4 1000 1000 1000 4 27 8 1000 1000 1000 1000 8 8 1000 1000 1000 8 1000 28 5 1000 1000 1000 1000 5 1000 1000 5 1000 1000 5 29 1000 1000 6 6 1000 1000 6 1000 1000 1000 1000 6 30 1000 1000 2 2 1000 1000 1000 1000 2 1000 2 1000 31 1000 6 1000 1000 6 1000 1000 1000 6 1000 6 1000 32 9 1000 1000 1000 9 1000 1000 9 1000 9 1000 1000 33 4 1000 1000 1000 1000 4 4 1000 1000 1000 4 1000 34 1000 2 1000 1000 2 1000 2 1000 1000 2 1000 1000 35 5 1000 1000 1000 1000 5 5 1000 1000 1000 5 1000 36 1000 1000 4 4 1000 1000 4 1000 1000 1000 1000 4 37 10 1000 1000 1000 1000 10 1000 1000 10 1000 1000 10 38 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 39 1000 1000 7 7 1000 1000 1000 1000 7 1000 7 1000 40 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 41 3 1000 1000 1000 1000 3 1000 1000 3 1000 1000 3 42 1000 8 1000 1000 8 1000 1000 1000 8 1000 8 1000 43 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 1000 44 4 1000 1000 1000 1000 4 4 1000 1000 1000 4 1000 45 1000 6 1000 1000 6 1000 6 1000 1000 6 1000 1000 46 1000 1000 4 4 1000 1000 4 1000 1000 1000 1000 4 47 8 1000 1000 1000 1000 8 8 1000 1000 1000 8 1000 48 5 1000 1000 1000 1000 5 1000 1000 5 1000 1000 5 49 1000 1000 6 6 1000 1000 1000 6 1000 1000 1000 6 50 1000 3 1000 1000 3 1000 1000 1000 3 1000 3 1000 | Predecessor Successor 1 2 3 4 2 5 4 5 6 7 7 8 5 9 8 9 10 12 11 12 13 16 14 16 15 16 12 17 16 17 18 19 20 21 22 23 19 24 21 24 23 24 25 26 26 27 27 28 28 29 29 30 31 33 32 33 34 36 35 36 37 39 38 39 36 40 39 40 41 42 43 44 42 45 44 45 46 47 47 48 48 49 49 50 | WorkStation Product Task Start_Time Completion_Time 1 P1 1 0 4 1 P6 35 5 7 1 P1 3 10 15 1 P1 7 17 21 1 P3 19 19 29 1 P2 12 21 17 2 P2 11 0 19 2 P1 6 10 30 2 P7 42 17 34 2 P6 40 31 13 3 P8 46 0 10 3 P2 15 12 29 3 P1 8 21 16 3 P1 9 30 28 4 P3 18 4 21 4 P4 26 9 32 4 P3 23 13 34 4 P3 20 16 9 4 P4 30 32 21 5 P4 25 0 21 5 P5 31 19 25 5 P3 24 25 9 6 P8 47 4 16 6 P1 4 15 31 6 P4 28 21 9 7 P6 34 6 13 7 P2 10 8 21 7 P4 27 13 26 7 P7 44 21 32 7 P2 14 25 34 7 P5 33 28 25 7 P2 17 32 9 8 P5 32 0 32 8 P2 13 9 8 8 P8 49 17 10 9 P3 22 0 14 9 P8 48 12 24 9 P1 5 21 4 9 P2 16 29 31 10 P7 43 11 34 10 P3 21 21 10 10 P7 45 25 25 11 P6 39 24 21 11 P8 50 31 25 12 P6 38 1 31 12 P1 2 4 4 12 P7 41 7 12 12 P6 36 10 17 12 P6 37 14 23 12 P4 29 26 34 |
| Utilization Rate: |
|---|
| Makespan = 34 Ws1: Total_Time=26.0, Utilization=0.7647 Ws2: Total_Time=28.0, Utilization=0.8235 Ws3: Total_Time=26.0, Utilization=0.7647 Ws4: Total_Time=19.0, Utilization=0.5588 Ws5: Total_Time=21.0, Utilization=0.6176 Ws6: Total_Time=19.0, Utilization=0.5588 Ws7: Total_Time=28.0, Utilization=0.8235 Ws8: Total_Time=22.0, Utilization=0.6471 Ws9: Total_Time=25.0, Utilization=0.7353 Ws10: Total_Time=20.0, Utilization=0.5882 Ws11: Total_Time=10.0, Utilization=0.2941 Ws12: Total_Time=29.0, Utilization=0.8529 Average System Utilization: 0.6691 |
Makespan = 34 Run-time = 528 seconds
Gantt Chart

Int_20
| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 1 1000 8 1000 1000 8 1000 1000 1000 8 1000 8 1000 2 5 1000 1000 1000 1000 5 5 1000 1000 1000 5 1000 3 1000 1000 7 7 1000 1000 1000 7 1000 1000 1000 7 4 1000 1000 3 3 1000 1000 3 1000 1000 1000 1000 3 5 2 1000 1000 1000 1000 2 1000 1000 2 1000 1000 2 6 1000 1000 10 10 1000 1000 1000 1000 10 1000 10 1000 7 1000 9 1000 1000 9 1000 9 1000 1000 9 1000 1000 8 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 9 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 1000 10 8 1000 1000 1000 1000 8 8 1000 1000 1000 8 1000 11 1000 1000 3 3 1000 1000 3 1000 1000 1000 1000 3 12 1000 5 1000 1000 5 1000 5 1000 1000 5 1000 1000 13 1000 1000 4 4 1000 1000 1000 1000 4 1000 4 1000 14 10 1000 1000 1000 1000 10 1000 1000 10 1000 1000 10 15 7 1000 1000 1000 7 1000 1000 7 1000 7 1000 1000 16 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 17 1000 1000 6 6 1000 1000 1000 6 1000 1000 1000 6 18 1000 1000 9 9 1000 1000 9 1000 1000 1000 1000 9 19 1000 10 1000 1000 10 1000 1000 1000 10 1000 10 1000 20 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 21 1000 1000 5 5 1000 1000 1000 1000 5 1000 5 1000 22 8 1000 1000 1000 1000 8 8 1000 1000 1000 8 1000 23 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 24 1000 1000 10 10 1000 1000 10 1000 1000 1000 1000 10 25 8 1000 1000 1000 1000 8 1000 1000 8 1000 1000 8 26 1000 1000 3 3 1000 1000 1000 1000 3 1000 3 1000 27 1000 4 1000 1000 4 1000 4 1000 1000 4 1000 1000 28 6 1000 1000 1000 6 1000 1000 6 1000 6 1000 1000 29 5 1000 1000 1000 1000 5 5 1000 1000 1000 5 1000 30 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 31 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 1000 32 1000 1000 6 6 1000 1000 1000 6 1000 1000 1000 6 33 8 1000 1000 1000 1000 8 1000 1000 8 1000 1000 8 34 7 1000 1000 1000 7 1000 1000 7 1000 7 1000 1000 35 9 1000 1000 1000 1000 9 9 1000 1000 1000 9 1000 36 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 37 8 1000 1000 1000 1000 8 1000 1000 8 1000 1000 8 38 1000 1000 2 2 1000 1000 2 1000 1000 1000 1000 2 39 1000 4 1000 1000 4 1000 4 1000 1000 4 1000 1000 40 1000 1000 5 5 1000 1000 1000 1000 5 1000 5 1000 41 1000 1000 5 5 1000 1000 1000 1000 5 1000 5 1000 42 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 43 7 1000 1000 1000 1000 7 7 1000 1000 1000 7 1000 44 6 1000 1000 1000 1000 6 1000 1000 6 1000 1000 6 45 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 46 1000 8 1000 1000 8 1000 8 1000 1000 8 1000 1000 47 9 1000 1000 1000 1000 9 1000 1000 9 1000 1000 9 48 3 1000 1000 1000 1000 3 3 1000 1000 1000 3 1000 49 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 1000 50 6 1000 1000 1000 1000 6 1000 1000 6 1000 1000 6 51 1000 1000 5 5 1000 1000 1000 5 1000 1000 1000 5 52 1000 10 1000 1000 10 1000 1000 1000 10 1000 10 1000 53 1000 1000 4 4 1000 1000 1000 1000 4 1000 4 1000 54 1000 1000 5 5 1000 1000 5 1000 1000 1000 1000 5 55 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 1000 | Predecessor Successor 1 2 3 4 2 5 4 5 6 7 7 8 5 9 8 9 10 12 11 12 13 16 14 16 15 16 12 17 16 17 19 21 20 21 18 23 21 23 22 23 24 25 25 26 26 27 27 28 28 29 30 31 31 33 32 33 34 36 35 36 37 39 38 39 36 40 39 40 41 42 43 44 42 45 44 45 46 47 47 48 48 49 49 50 50 51 52 53 53 54 54 55 | WorkStation Product Task Start_Time Completion_Time 1 P2 10 0 10 1 P8 47 8 15 1 P6 35 17 17 1 P1 9 32 30 2 P1 1 2 32 2 P1 7 10 10 2 P4 27 21 19 2 P3 23 34 26 3 P6 38 0 36 3 P1 3 10 8 3 P3 18 17 10 3 P6 36 26 19 3 P6 40 31 4 4 P1 6 0 23 4 P7 41 15 20 4 P9 53 20 25 4 P7 45 24 35 4 P1 4 27 26 4 P8 51 31 24 5 P8 46 0 29 5 P6 39 13 34 5 P5 31 17 15 5 P7 42 21 36 5 P2 16 23 10 6 P6 37 0 18 6 P2 14 13 21 6 P5 33 23 25 6 P4 29 31 31 7 P4 24 0 36 7 P1 2 10 17 7 P8 48 17 21 7 P1 8 20 7 8 P2 15 13 31 8 P8 49 20 26 8 P4 28 25 26 9 P2 13 0 29 9 P9 52 4 8 9 P3 19 14 2 9 P8 50 24 17 9 P1 5 30 36 10 P2 12 14 20 10 P6 34 19 23 10 P3 20 26 7 10 P9 55 29 24 11 P7 43 0 27 11 P3 22 7 8 11 P5 30 15 17 11 P4 26 18 20 11 P3 21 29 24 12 P5 32 1 30 12 P2 11 7 36 12 P4 25 10 14 12 P7 44 18 24 12 P9 54 24 29 12 P2 17 29 33 |
| Utilization Rate: |
|---|
| Makespan = 36 Ws1: Total_Time=20.0, Utilization=0.8696 Ws2: Total_Time=20.0, Utilization=0.8696 WWs1: Total_Time=30.0, Utilization=0.8333 Ws2: Total_Time=23.0, Utilization=0.6389 Ws3: Total_Time=26.0, Utilization=0.7222 Ws4: Total_Time=30.0, Utilization=0.8333 Ws5: Total_Time=20.0, Utilization=0.5556 Ws6: Total_Time=31.0, Utilization=0.8611 Ws7: Total_Time=24.0, Utilization=0.6667 Ws8: Total_Time=17.0, Utilization=0.4722 Ws9: Total_Time=32.0, Utilization=0.8889 Ws10: Total_Time=19.0, Utilization=0.5278 Ws11: Total_Time=25.0, Utilization=0.6944 Ws12: Total_Time=34.0, Utilization=0.9444 Average System Utilization: 0.7199 |
Makespan = 36 Run-time = 348 seconds
Gantt Chart

Int_21
| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 1 1000 1000 8 8 1000 1000 8 1000 1000 1000 1000 8 2 10 1000 1000 1000 1000 10 10 1000 1000 1000 10 1000 3 1000 6 1000 1000 6 1000 1000 1000 6 1000 6 1000 4 7 1000 1000 1000 7 1000 1000 7 1000 7 1000 1000 5 3 1000 1000 1000 1000 3 1000 1000 3 1000 1000 3 6 1000 1000 5 5 1000 1000 1000 5 1000 1000 1000 5 7 1000 4 1000 1000 4 1000 4 1000 1000 4 1000 1000 8 1000 4 1000 1000 4 1000 1000 1000 4 1000 4 1000 9 1000 1000 2 2 1000 1000 1000 1000 2 1000 2 1000 10 8 1000 1000 1000 8 1000 1000 8 1000 8 1000 1000 11 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 12 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 13 9 1000 1000 1000 1000 9 1000 1000 9 1000 1000 9 14 1000 1000 5 5 1000 1000 5 1000 1000 1000 1000 5 15 1000 1000 7 7 1000 1000 1000 7 1000 1000 1000 7 16 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 1000 17 1000 1000 4 4 1000 1000 1000 4 1000 1000 1000 4 18 1000 8 1000 1000 8 1000 8 1000 1000 8 1000 1000 19 6 1000 1000 1000 1000 6 1000 1000 6 1000 1000 6 20 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 21 1000 1000 3 3 1000 1000 3 1000 1000 1000 1000 3 22 1000 1000 9 9 1000 1000 1000 1000 9 1000 9 1000 23 5 1000 1000 1000 1000 5 5 1000 1000 1000 5 1000 24 8 1000 1000 1000 1000 8 8 1000 1000 1000 8 1000 25 1000 9 1000 1000 9 1000 1000 1000 9 1000 9 1000 26 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 1000 27 5 1000 1000 1000 1000 5 1000 1000 5 1000 1000 5 28 1000 1000 6 6 1000 1000 1000 6 1000 1000 1000 6 29 1000 1000 4 4 1000 1000 1000 1000 4 1000 4 1000 30 1000 4 1000 1000 4 1000 4 1000 1000 4 1000 1000 31 3 1000 1000 1000 1000 3 3 1000 1000 1000 3 1000 32 1000 1000 6 6 1000 1000 6 1000 1000 1000 1000 6 33 1000 1000 8 8 1000 1000 1000 8 1000 1000 1000 8 34 5 1000 1000 1000 1000 5 1000 1000 5 1000 1000 5 35 1000 1000 4 4 1000 1000 1000 1000 4 1000 4 1000 36 7 1000 1000 1000 7 1000 1000 7 1000 7 1000 1000 37 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 38 8 1000 1000 1000 1000 8 1000 1000 8 1000 1000 8 39 1000 10 1000 1000 10 1000 1000 1000 10 1000 10 1000 40 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 1000 41 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 42 1000 1000 7 7 1000 1000 1000 1000 7 1000 7 1000 43 9 1000 1000 1000 9 1000 1000 9 1000 9 1000 1000 44 1000 1000 4 4 1000 1000 4 1000 1000 1000 1000 4 45 3 1000 1000 1000 1000 3 1000 1000 3 1000 1000 3 46 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 47 8 1000 1000 1000 8 1000 1000 8 1000 8 1000 1000 48 1000 1000 3 3 1000 1000 1000 1000 3 1000 3 1000 49 1000 1000 5 5 1000 1000 5 1000 1000 1000 1000 5 50 1000 1000 9 9 1000 1000 1000 9 1000 1000 1000 9 51 1000 2 1000 1000 2 1000 2 1000 1000 2 1000 1000 52 1000 1000 10 10 1000 1000 1000 10 1000 1000 1000 10 53 7 1000 1000 1000 1000 7 1000 1000 7 1000 1000 7 54 9 1000 1000 1000 9 1000 1000 9 1000 9 1000 1000 55 6 1000 1000 1000 1000 6 6 1000 1000 1000 6 1000 56 10 1000 1000 1000 1000 10 1000 1000 10 1000 1000 10 57 1000 1000 3 3 1000 1000 1000 3 1000 1000 1000 3 58 1000 1000 4 4 1000 1000 4 1000 1000 1000 1000 4 59 1000 6 1000 1000 6 1000 6 1000 1000 6 1000 1000 60 1000 2 1000 1000 2 1000 1000 1000 2 1000 2 1000 | Predecessor Successor 1 3 2 3 4 5 5 6 3 7 6 7 8 10 9 10 11 14 12 14 13 14 10 15 14 15 17 18 19 20 18 21 20 21 16 23 21 23 22 23 24 25 25 26 26 27 27 28 28 29 30 32 31 32 34 35 33 36 35 36 32 37 36 37 38 40 39 40 41 42 43 44 42 45 44 45 46 47 47 48 48 49 49 50 50 51 52 53 53 54 54 55 56 58 57 58 58 60 59 60 | WorkStation Product Task Start_Time Completion_Time 1 P10 56 0 8 1 P7 41 13 10 1 P2 10 19 24 1 P4 27 27 7 1 P7 45 35 10 1 P6 40 38 25 2 P4 25 8 42 2 P5 37 34 14 2 P1 7 38 15 3 P9 52 0 27 3 P5 32 11 29 3 P8 50 23 20 3 P4 28 32 27 3 P4 29 38 34 4 P1 1 0 42 4 P3 22 8 17 4 P2 12 17 10 4 P1 6 20 22 4 P7 44 25 6 4 P10 57 29 24 4 P3 21 32 35 4 P2 15 35 17 5 P6 39 0 40 5 P2 8 10 8 5 P3 18 14 17 5 P3 20 22 27 5 P9 54 24 32 6 P8 46 0 38 6 P1 5 7 42 6 P5 34 10 4 6 P9 53 15 11 6 P6 38 22 17 6 P9 55 33 18 7 P4 24 0 15 7 P5 31 8 19 7 P10 59 12 34 7 P8 49 18 36 7 P2 11 23 30 7 P2 14 29 10 7 P10 58 34 42 7 P8 51 40 19 8 P1 4 0 35 8 P8 47 7 25 8 P7 43 16 29 9 P2 9 13 38 9 P8 48 15 6 9 P1 3 18 15 9 P7 42 28 18 10 P5 30 0 23 10 P3 16 7 32 10 P4 26 17 42 10 P5 36 27 10 11 P1 2 0 22 11 P5 35 15 33 11 P3 23 35 39 11 P10 60 40 10 12 P3 19 0 32 12 P3 17 6 38 12 P5 33 10 18 12 P3 20 22 42 |
| Utilization Rate: |
|---|
| Makespan = 42 Ws1: Total_Time=36.0, Utilization=0.8571 Ws2: Total_Time=15.0, Utilization=0.3571 Ws3: Total_Time=35.0, Utilization=0.8333 Ws4: Total_Time=42.0, Utilization=1.0000 Ws5: Total_Time=33.0, Utilization=0.7857 Ws6: Total_Time=35.0, Utilization=0.8333 Ws7: Total_Time=39.0, Utilization=0.9286 Ws8: Total_Time=24.0, Utilization=0.5714 Ws9: Total_Time=18.0, Utilization=0.4286 Ws10: Total_Time=31.0, Utilization=0.7381 Ws11: Total_Time=21.0, Utilization=0.5000 Ws12: Total_Time=20.0, Utilization=0.4762 Average System Utilization: 0.6925 |
Makespan = 42 Run-time = 3932 seconds
Gantt Chart

Matrix-Structure 4 x 4
Int_22
| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 Ws13 Ws14 Ws15 Ws16 1 1000 8 1000 8 1000 8 1000 1000 8 1000 8 1000 1000 8 1000 1000 2 1000 1000 4 4 1000 4 1000 4 4 1000 1000 1000 1000 1000 4 1000 3 1000 10 1000 1000 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 10 4 1000 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 1000 6 5 7 1000 1000 7 1000 7 1000 1000 1000 1000 7 1000 7 1000 1000 7 6 1000 2 1000 1000 1000 1000 2 2 1000 1000 2 1000 1000 2 1000 2 7 3 1000 1000 3 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 8 1000 1000 5 1000 5 1000 1000 5 1000 5 1000 5 5 1000 1000 1000 9 2 1000 1000 1000 1000 1000 2 1000 2 1000 2 1000 1000 2 2 1000 10 1000 2 2 1000 1000 2 1000 1000 1000 1000 1000 2 2 1000 2 1000 11 8 1000 1000 8 1000 8 1000 1000 1000 1000 8 1000 8 1000 1000 8 12 5 1000 1000 5 5 1000 1000 5 1000 5 1000 1000 1000 1000 5 1000 13 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 6 1000 1000 14 1000 1000 9 9 1000 9 1000 9 9 1000 1000 1000 1000 1000 9 1000 15 4 1000 100011000 1000 1000 4 1000 4 1000 4 1000 1000 4 4 1000 16 1000 1000 7 1000 7 1000 7 1000 1000 7 1000 7 1000 1000 1000 7 17 1000 3 1000 1000 3 1000 1000 1000 3 1000 1000 3 1000 3 1000 3 18 1000 10 1000 1000 1000 1000 10 10 1000 1000 10 1000 1000 10 1000 10 19 1000 1000 6 1000 6 1000 1000 6 1000 6 1000 6 6 1000 1000 1000 20 1000 2 2 1000 1000 2 1000 1000 1000 1000 1000 2 2 1000 2 1000 21 8 1000 1000 1000 1000 1000 8 1000 8 1000 8 1000 1000 8 8 1000 22 3 1000 1000 3 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 23 1000 4 1000 4 1000 4 1000 1000 4 1000 4 1000 1000 4 1000 1000 24 5 1000 1000 5 1000 5 1000 1000 1000 1000 5 1000 5 1000 1000 5 25 1000 1000 4 1000 4 1000 4 1000 1000 4 1000 4 1000 1000 1000 4 26 1000 2 1000 1000 2 1000 1000 1000 2 1000 1000 2 1000 2 1000 2 27 4 1000 1000 4 1000 4 1000 1000 1000 1000 4 1000 4 1000 1000 4 28 1000 3 3 1000 1000 3 1000 1000 1000 1000 1000 3 3 1000 3 1000 29 1000 5 1000 5 1000 5 1000 1000 5 1000 5 1000 1000 5 1000 1000 30 1000 1000 2 2 1000 2 1000 2 2 1000 1000 1000 1000 1000 2 1000 31 10 1000 1000 10 10 1000 1000 10 1000 10 1000 1000 1000 1000 10 1000 32 4 1000 1000 4 1000 4 1000 1000 1000 1000 4 1000 4 1000 1000 4 33 6 1000 1000 1000 1000 1000 6 1000 6 1000 6 1000 1000 6 6 1000 34 1000 1000 7 1000 7 1000 7 1000 1000 7 1000 7 1000 1000 1000 7 35 1000 1000 5 1000 5 1000 1000 5 1000 5 1000 5 5 1000 1000 1000 36 1000 8 8 1000 1000 8 1000 1000 1000 1000 1000 8 8 1000 8 1000 37 6 1000 1000 1000 1000 1000 6 1000 6 1000 6 1000 1000 6 6 1000 38 9 1000 1000 9 1000 9 1000 1000 1000 1000 9 1000 9 1000 1000 9 39 4 1000 1000 4 4 1000 1000 4 1000 4 1000 1000 1000 1000 4 1000 40 1000 1000 3 1000 3 1000 3 1000 1000 3 1000 3 1000 1000 1000 3 41 1000 10 1000 10 1000 10 1000 1000 10 1000 10 1000 1000 10 1000 1000 42 1000 3 1000 1000 3 1000 1000 1000 3 1000 1000 3 1000 3 1000 3 43 5 1000 1000 5 1000 5 1000 1000 1000 1000 5 1000 5 1000 1000 5 44 1000 9 1000 1000 1000 1000 9 9 1000 1000 9 1000 1000 9 1000 9 45 1000 1000 6 6 1000 6 1000 6 6 1000 1000 1000 1000 1000 6 1000 46 1000 2 1000 2 1000 2 1000 1000 2 1000 2 1000 1000 2 1000 1000 47 1000 1000 6 6 1000 6 1000 6 6 1000 1000 1000 1000 1000 6 1000 48 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 3 1000 1000 3 49 5 1000 1000 5 5 1000 1000 5 1000 5 1000 1000 1000 1000 5 1000 50 1000 4 4 1000 1000 4 1000 1000 1000 1000 1000 4 4 1000 4 1000 | Predecessor Successor 1 2 2 4 3 4 5 6 6 7 7 8 4 9 8 9 10 12 11 12 13 16 14 16 15 16 12 17 16 17 18 20 19 20 21 22 20 23 22 23 23 24 25 26 26 27 27 28 28 29 29 30 31 33 32 33 34 36 35 36 37 39 38 39 36 40 39 40 41 42 43 44 42 45 44 45 46 47 47 48 48 49 49 50 | WorkStation Product Task Start_Time Completion_Time 1 P2 11 0 8 1 P3 22 8 12 1 P8 49 11 10 1 P3 24 16 18 2 P7 41 0 7 2 P3 20 10 11 2 P3 23 12 14 3 P6 34 0 19 3 P1 2 8 21 3 P1 8 14 2 4 P1 5 0 8 4 P4 27 7 15 4 P5 32 11 9 5 P4 25 0 9 5 P3 19 4 11 5 P1 7 11 18 5 P6 39 14 21 5 P2 17 18 10 6 P1 1 0 10 6 P8 48 8 12 6 P4 28 11 8 6 P8 50 17 11 7 P3 21 0 16 7 P6 37 8 21 8 P6 35 0 4 8 P7 44 5 6 8 P7 45 14 11 9 P2 14 0 14 9 P7 42 11 19 9 P4 30 19 21 10 P5 31 0 10 10 P2 12 10 15 11 P8 46 0 21 11 P2 13 3 7 11 P1 6 9 5 11 P4 29 14 18 11 P1 9 19 14 12 P1 3 0 14 12 P2 16 11 18 12 P6 40 18 21 13 P7 43 0 10 13 P6 38 5 14 14 P4 26 4 5 14 P2 15 7 14 14 P5 33 15 20 15 P2 10 0 2 15 P8 47 2 8 15 P6 36 10 11 16 P3 18 0 16 16 P1 4 12 21 |
| Utilization Rate: |
|---|
| Makespan = 21 Ws1: Total_Time=21.0, Utilization=1.0000 Ws2: Total_Time=16.0, Utilization=0.7619 Ws3: Total_Time=16.0, Utilization=0.7619 Ws4: Total_Time=15.0, Utilization=0.7143 Ws5: Total_Time=20.0, Utilization=0.9524 Ws6: Total_Time=18.0, Utilization=0.8571 Ws7: Total_Time=14.0, Utilization=0.6667 Ws8: Total_Time=20.0, Utilization=0.9524 Ws9: Total_Time=14.0, Utilization=0.6667 Ws10: Total_Time=15.0, Utilization=0.7143 Ws11: Total_Time=17.0, Utilization=0.8095 Ws12: Total_Time=20.0, Utilization=0.9524 Ws13: Total_Time=14.0, Utilization=0.6667 Ws14: Total_Time=12.0, Utilization=0.5714 Ws15: Total_Time=16.0, Utilization=0.7619 Ws16: Total_Time=16.0, Utilization=0.7619 Average System Utilization: 0.7857 |
Makespan = 21 Run-time = 344 seconds
Gantt Chart

Int_23

| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 Ws13 Ws14 Ws15 Ws16 1 1000 5 1000 1000 5 1000 1000 1000 5 1000 1000 5 1000 5 1000 5 2 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 6 1000 1000 3 10 1000 1000 10 1000 10 1000 1000 1000 1000 10 1000 10 1000 1000 10 4 4 1000 1000 1000 1000 1000 4 1000 4 1000 4 1000 1000 4 4 1000 5 8 1000 1000 8 8 1000 1000 8 1000 8 1000 1000 1000 1000 8 1000 6 1000 1000 7 1000 7 1000 1000 7 1000 7 1000 7 7 1000 1000 1000 7 1000 1000 3 3 1000 3 1000 3 3 1000 1000 1000 1000 1000 3 1000 8 1000 9 9 1000 1000 9 1000 1000 1000 1000 1000 9 9 1000 9 1000 9 1000 2 1000 1000 1000 1000 2 2 1000 1000 2 1000 1000 2 1000 2 10 1000 1000 5 1000 5 1000 5 1000 1000 5 1000 5 1000 1000 1000 5 11 6 1000 1000 1000 1000 1000 6 1000 6 1000 6 1000 1000 6 6 1000 12 8 1000 1000 8 1000 8 1000 1000 1000 1000 8 1000 8 1000 1000 8 13 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 14 1000 7 7 1000 1000 7 1000 1000 1000 1000 1000 7 7 1000 7 1000 15 3 1000 1000 3 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 16 1000 5 1000 5 1000 5 1000 1000 5 1000 5 1000 1000 5 1000 1000 17 1000 1000 10 1000 10 1000 10 1000 1000 10 1000 10 1000 1000 1000 10 18 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 3 1000 1000 3 19 1000 1000 4 4 1000 4 1000 4 4 1000 1000 1000 1000 1000 4 1000 20 8 1000 1000 8 8 1000 1000 8 1000 8 1000 1000 1000 1000 8 1000 21 1000 1000 6 1000 6 1000 1000 6 1000 6 1000 6 6 1000 1000 1000 22 1000 7 1000 1000 1000 1000 7 7 1000 1000 7 1000 1000 7 1000 7 23 2 1000 1000 1000 1000 1000 2 1000 2 1000 2 1000 1000 2 2 1000 24 1000 2 2 1000 1000 2 1000 1000 1000 1000 1000 2 2 1000 2 1000 25 1000 5 1000 1000 5 1000 1000 1000 5 1000 1000 5 1000 5 1000 5 26 1000 3 1000 3 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 27 4 1000 1000 4 4 1000 1000 4 1000 4 1000 1000 1000 1000 4 1000 28 6 1000 1000 1000 1000 1000 6 1000 6 1000 6 1000 1000 6 6 1000 29 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 3 1000 1000 3 30 1000 10 1000 1000 1000 1000 10 10 1000 1000 10 1000 1000 10 1000 10 31 3 1000 1000 1000 1000 1000 3 1000 3 1000 3 1000 1000 3 3 1000 32 1000 1000 5 1000 5 1000 1000 5 1000 5 1000 5 5 1000 1000 1000 33 1000 1000 7 7 1000 7 1000 7 7 1000 1000 1000 1000 1000 7 1000 34 1000 8 1000 1000 8 1000 1000 1000 8 1000 1000 8 1000 8 1000 8 35 1000 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 1000 6 36 4 1000 1000 4 4 1000 1000 4 1000 4 1000 1000 1000 1000 4 1000 37 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 6 1000 1000 38 1000 3 3 1000 1000 3 1000 1000 1000 1000 1000 3 3 1000 3 1000 39 9 1000 1000 1000 1000 1000 9 1000 9 1000 9 1000 1000 9 9 1000 40 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 41 1000 1000 3 3 1000 3 1000 3 3 1000 1000 1000 1000 1000 3 1000 42 10 1000 1000 10 1000 10 1000 1000 1000 1000 10 1000 10 1000 1000 10 43 1000 9 1000 1000 1000 1000 9 9 1000 1000 9 1000 1000 9 1000 9 44 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 45 1000 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 1000 6 46 1000 8 8 1000 1000 8 1000 1000 1000 1000 1000 8 8 1000 8 1000 47 3 1000 1000 3 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 48 1000 1000 7 7 1000 7 1000 7 7 1000 1000 1000 1000 1000 7 1000 49 1000 2 1000 2 1000 2 1000 1000 2 1000 2 1000 1000 2 1000 1000 50 1000 1000 3 1000 3 1000 1000 3 1000 3 1000 3 3 1000 1000 1000 51 1000 5 1000 5 1000 5 1000 1000 5 1000 5 1000 1000 5 1000 1000 52 1000 1000 7 1000 7 1000 7 1000 1000 7 1000 7 1000 1000 1000 7 53 1000 2 1000 1000 1000 1000 2 2 1000 1000 2 1000 1000 2 1000 2 54 1000 1000 3 3 1000 3 1000 3 3 1000 1000 1000 1000 1000 3 1000 55 1000 6 6 1000 1000 6 1000 1000 1000 1000 1000 6 6 1000 6 1000 | Predecessor Successor 1 2 2 4 3 4 5 6 5 7 6 7 8 9 9 11 10 11 12 15 13 15 14 15 11 16 15 16 18 19 19 21 20 21 17 23 21 23 22 23 24 25 25 26 26 27 27 28 28 29 30 32 31 32 33 35 34 35 32 36 35 36 37 38 38 40 39 40 41 42 43 44 42 45 44 45 46 47 47 48 48 49 49 50 51 52 52 53 53 54 54 55 | WorkStation Product Task Start_Time Completion_Time 1 P2 12 3 5 1 P2 11 12 11 2 P2 13 0 19 2 P5 34 4 23 3 P2 8 0 8 3 P3 19 9 19 3 P5 35 13 23 4 P6 37 0 9 4 P3 18 6 12 4 P1 3 9 5 5 P1 5 0 18 5 P4 27 10 11 5 P5 32 14 4 5 P6 40 19 10 6 P8 46 0 14 6 P8 48 11 23 7 P5 31 0 20 7 P7 43 3 9 7 P9 53 12 13 7 P3 22 14 8 7 P3 23 21 20 8 P7 41 0 21 8 P1 6 12 23 8 P5 36 19 2 9 P1 1 0 7 9 P5 33 5 10 9 P9 54 14 14 9 P8 49 18 20 9 P1 7 20 23 10 P3 20 0 10 10 P8 47 8 3 10 P2 15 11 19 10 P3 21 14 12 10 P8 50 20 12 11 P9 51 0 19 11 P1 2 5 23 11 P4 28 14 6 12 P2 10 0 17 12 P9 52 5 19 12 P7 45 17 23 13 P4 24 0 3 13 P7 42 3 13 13 P6 38 14 12 13 P9 55 17 17 14 P4 25 2 23 14 P4 26 7 8 14 P2 9 10 11 14 P7 44 13 18 14 P2 16 18 20 15 P2 14 3 23 15 P6 39 10 5 15 P1 4 19 12 16 P5 30 0 14 16 P3 17 10 17 16 P4 29 20 23 |
| Utilization Rate: |
|---|
| Makespan = 23 Ws1: Total_Time=14.0, Utilization=0.6087 Ws2: Total_Time=12.0, Utilization=0.5217 Ws3: Total_Time=19.0, Utilization=0.8261 Ws4: Total_Time=19.0, Utilization=0.8261 Ws5: Total_Time=21.0, Utilization=0.9130 Ws6: Total_Time=15.0, Utilization=0.6522 Ws7: Total_Time=23.0, Utilization=1.0000 Ws8: Total_Time=14.0, Utilization=0.6087 Ws9: Total_Time=20.0, Utilization=0.8696 Ws10: Total_Time=23.0, Utilization=1.0000 Ws11: Total_Time=17.0, Utilization=0.7391 Ws12: Total_Time=18.0, Utilization=0.7826 Ws13: Total_Time=21.0, Utilization=0.9130 Ws14: Total_Time=19.0, Utilization=0.8261 Ws15: Total_Time=20.0, Utilization=0.8696 Ws16: Total_Time=23.0, Utilization=1.0000 Average System Utilization: 0.8098 |
Makespan = 23 Run-time = 482 seconds
Gantt Chart

Int_24

| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 Ws13 Ws14 Ws15 Ws16 1 6 1000 1000 6 6 1000 1000 6 1000 6 1000 1000 1000 1000 6 1000 2 7 1000 1000 1000 1000 1000 7 1000 7 1000 7 1000 1000 7 7 1000 3 1000 9 1000 9 1000 9 1000 1000 9 1000 9 1000 1000 9 1000 1000 4 1000 3 1000 1000 3 1000 1000 1000 3 1000 1000 3 1000 3 1000 3 5 1000 1000 5 5 1000 5 1000 5 5 1000 1000 1000 1000 1000 5 1000 6 1000 1000 4 1000 4 1000 4 1000 1000 4 1000 4 1000 1000 1000 4 7 1000 2 2 1000 1000 2 1000 1000 1000 1000 1000 2 2 1000 2 1000 8 8 1000 1000 8 1000 8 1000 1000 1000 1000 8 1000 8 1000 1000 8 9 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 10 1000 5 1000 1000 1000 1000 5 5 1000 1000 5 1000 1000 5 1000 5 11 1000 1000 9 1000 9 1000 1000 9 1000 9 1000 9 9 1000 1000 1000 12 10 1000 1000 10 10 1000 1000 10 1000 10 1000 1000 1000 1000 10 1000 13 7 1000 1000 1000 1000 1000 7 1000 7 1000 7 1000 1000 7 7 1000 14 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 6 1000 1000 15 1000 1000 3 3 1000 3 1000 3 3 1000 1000 1000 1000 1000 3 1000 16 1000 4 4 1000 1000 4 1000 1000 1000 1000 1000 4 4 1000 4 1000 17 1000 1000 2 1000 2 1000 2 1000 1000 2 1000 2 1000 1000 1000 2 18 1000 1000 5 1000 5 1000 1000 5 1000 5 1000 5 5 1000 1000 1000 19 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 3 1000 1000 3 20 10 1000 1000 1000 1000 1000 10 1000 10 1000 10 1000 1000 10 10 1000 21 1000 8 1000 1000 8 1000 1000 1000 8 1000 1000 8 1000 8 1000 8 22 1000 1000 7 7 1000 7 1000 7 7 1000 1000 1000 1000 1000 7 1000 23 6 1000 1000 6 6 1000 1000 6 1000 6 1000 1000 1000 1000 6 1000 24 1000 4 1000 1000 1000 1000 4 4 1000 1000 4 1000 1000 4 1000 4 25 1000 3 1000 3 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 26 7 1000 1000 7 1000 7 1000 1000 1000 1000 7 1000 7 1000 1000 7 27 2 1000 1000 1000 1000 1000 2 1000 2 1000 2 1000 1000 2 2 1000 28 1000 6 6 1000 1000 6 1000 1000 1000 1000 1000 6 6 1000 6 1000 29 1000 1000 3 1000 3 1000 1000 3 1000 3 1000 3 3 1000 1000 1000 30 1000 1000 5 5 1000 5 1000 5 5 1000 1000 1000 1000 1000 5 1000 31 1000 1000 8 1000 8 1000 8 1000 1000 8 1000 8 1000 1000 1000 8 32 6 1000 1000 6 1000 6 1000 1000 1000 1000 6 1000 6 1000 1000 6 33 9 1000 1000 9 9 1000 1000 9 1000 9 1000 1000 1000 1000 9 1000 34 1000 3 3 1000 1000 3 1000 1000 1000 1000 1000 3 3 1000 3 1000 35 1000 2 1000 2 1000 2 1000 1000 2 1000 2 1000 1000 2 1000 1000 36 1000 4 1000 1000 1000 1000 4 4 1000 1000 4 1000 1000 4 1000 4 37 1000 1000 5 1000 5 1000 1000 5 1000 5 1000 5 5 1000 1000 1000 38 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 39 10 1000 1000 10 10 1000 1000 10 1000 10 1000 1000 1000 1000 10 1000 40 1000 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 1000 6 41 1000 8 1000 8 1000 8 1000 1000 8 1000 8 1000 1000 8 1000 1000 42 1000 2 1000 1000 1000 1000 2 2 1000 1000 2 1000 1000 2 1000 2 43 1000 3 1000 1000 3 1000 1000 1000 3 1000 1000 3 1000 3 1000 3 44 1000 9 9 1000 1000 9 1000 1000 1000 1000 1000 9 9 1000 9 1000 45 7 1000 1000 7 1000 7 1000 1000 1000 1000 7 1000 7 1000 1000 7 46 3 1000 1000 3 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 47 2 1000 1000 1000 1000 1000 2 1000 2 1000 2 1000 1000 2 2 1000 48 1000 4 4 1000 1000 4 1000 1000 1000 1000 1000 4 4 1000 4 1000 49 1000 8 1000 1000 1000 1000 8 8 1000 1000 8 1000 1000 8 1000 8 50 1000 1000 6 6 1000 6 1000 6 6 1000 1000 1000 1000 1000 6 1000 51 1000 2 1000 2 1000 2 1000 1000 2 1000 2 1000 1000 2 1000 1000 52 1000 1000 9 1000 9 1000 1000 9 1000 9 1000 9 9 1000 1000 1000 53 4 1000 1000 4 1000 4 1000 1000 1000 1000 4 1000 4 1000 1000 4 54 1000 5 1000 1000 5 1000 1000 1000 5 1000 1000 5 1000 5 1000 5 55 6 1000 1000 1000 1000 1000 6 1000 6 1000 6 1000 1000 6 6 1000 56 1000 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 1000 6 57 1000 7 1000 7 1000 7 1000 1000 7 1000 7 1000 1000 7 1000 1000 58 1000 2 1000 1000 1000 1000 2 2 1000 1000 2 1000 1000 2 1000 2 59 10 1000 1000 1000 1000 1000 10 1000 10 1000 10 1000 1000 10 10 1000 60 1000 5 1000 1000 5 1000 1000 1000 5 1000 1000 5 1000 5 1000 5 | Predecessor Successor 1 2 2 4 3 4 5 6 4 7 6 7 8 10 9 10 11 14 12 14 13 14 10 15 14 15 17 18 18 19 19 21 20 21 16 23 21 23 22 23 24 25 25 26 26 27 27 28 28 29 30 32 31 32 33 35 34 35 32 36 35 36 37 38 38 40 39 40 41 42 43 44 42 45 44 45 46 47 47 48 48 49 49 50 50 51 52 53 53 54 54 55 56 58 57 58 58 60 59 60 | WorkStation Product Task Start_Time Completion_Time 1 P2 12 0 6 1 P9 53 10 15 1 P4 27 14 9 1 P7 45 18 23 2 P5 34 0 5 2 P4 25 4 23 2 P7 44 9 25 2 P5 36 21 15 3 P1 5 0 7 3 P8 48 5 22 3 P3 22 9 9 3 P8 50 17 10 4 P1 1 0 16 4 P4 26 7 22 4 P2 14 16 25 4 P2 15 22 19 5 P2 11 0 2 5 P4 29 22 8 6 P10 57 0 11 6 P2 8 7 10 6 P5 32 15 19 6 P1 7 23 16 7 P10 59 0 25 7 P10 56 10 4 7 P10 58 17 7 7 P6 40 19 14 8 P4 24 0 16 8 P5 30 4 22 8 P8 49 9 25 8 P2 10 17 9 9 P7 41 0 10 9 P1 2 8 21 9 P1 4 20 15 10 P8 46 0 3 10 P3 18 3 20 10 P6 39 8 25 10 P3 23 19 14 11 P1 3 0 18 11 P2 13 9 18 11 P7 42 16 25 11 P5 35 18 8 12 P3 17 0 18 12 P5 31 2 3 12 P3 21 11 18 12 P10 60 20 25 13 P9 52 0 3 13 P6 37 9 5 13 P4 28 16 9 14 P3 20 0 17 14 P6 38 14 23 14 P8 51 23 25 15 P8 47 3 9 15 P5 33 6 14 15 P3 16 15 19 15 P9 55 19 25 16 P7 43 0 16 16 P2 9 3 7 16 P3 19 8 19 16 P9 54 14 10 16 P1 6 19 25 |
| Utilization Rate: |
|---|
| Makespan = 25 Ws1: Total_Time=23.0, Utilization=0.9200 Ws2: Total_Time=19.0, Utilization=0.7600 Ws3: Total_Time=22.0, Utilization=0.8800 Ws4: Total_Time=22.0, Utilization=0.8800 Ws5: Total_Time=12.0, Utilization=0.4800 Ws6: Total_Time=23.0, Utilization=0.9200 Ws7: Total_Time=24.0, Utilization=0.9600 Ws8: Total_Time=22.0, Utilization=0.8800 Ws9: Total_Time=18.0, Utilization=0.7200 Ws10: Total_Time=24.0, Utilization=0.9600 Ws11: Total_Time=20.0, Utilization=0.8000 Ws12: Total_Time=23.0, Utilization=0.9200 Ws13: Total_Time=20.0, Utilization=0.8000 Ws14: Total_Time=16.0, Utilization=0.6400 Ws15: Total_Time=21.0, Utilization=0.8400 Ws16: Total_Time=19.0, Utilization=0.7600 Average System Utilization: 0.8200 |
Makespan = 25 Run-time = 579 seconds
Gantt Chart

Int_25

| Input Data: Processing Time | List of Precedents: | Output Data: |
|---|---|---|
| Tasks Ws1 Ws2 Ws3 Ws4 Ws5 Ws6 Ws7 Ws8 Ws9 Ws10 Ws11 Ws12 Ws13 Ws14 Ws15 Ws16 1 6 1000 1000 1000 1000 1000 6 1000 6 1000 6 1000 1000 6 6 1000 2 1000 8 8 1000 1000 8 1000 1000 1000 1000 1000 8 8 1000 8 1000 3 1000 10 1000 1000 10 1000 1000 1000 10 1000 1000 10 1000 10 1000 10 4 9 1000 1000 9 1000 9 1000 1000 1000 1000 9 1000 9 1000 1000 9 5 1000 1000 3 1000 3 1000 3 1000 1000 3 1000 3 1000 1000 1000 3 6 1000 7 1000 7 1000 7 1000 1000 7 1000 7 1000 1000 7 1000 1000 7 1000 1000 5 5 1000 5 1000 5 5 1000 1000 1000 1000 1000 5 1000 8 1000 4 1000 1000 1000 1000 4 4 1000 1000 4 1000 1000 4 1000 4 9 1000 1000 2 1000 2 1000 1000 2 1000 2 1000 2 2 1000 1000 1000 10 1000 1000 8 1000 8 1000 8 1000 1000 8 1000 8 1000 1000 1000 8 11 4 1000 1000 4 4 1000 1000 4 1000 4 1000 1000 1000 1000 4 1000 12 1000 5 5 1000 1000 5 1000 1000 1000 1000 1000 5 5 1000 5 1000 13 9 1000 1000 1000 1000 1000 9 1000 9 1000 9 1000 1000 9 9 1000 14 1000 1000 10 10 1000 10 1000 10 10 1000 1000 1000 1000 1000 10 1000 15 1000 7 1000 1000 7 1000 1000 1000 7 1000 1000 7 1000 7 1000 7 16 1000 1000 6 1000 6 1000 1000 6 1000 6 1000 6 6 1000 1000 1000 17 1000 3 1000 3 1000 3 1000 1000 3 1000 3 1000 1000 3 1000 1000 18 1000 5 1000 1000 5 1000 1000 1000 5 1000 1000 5 1000 5 1000 5 19 3 1000 1000 3 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 20 4 1000 1000 1000 1000 1000 4 1000 4 1000 4 1000 1000 4 4 1000 21 1000 1000 2 1000 2 1000 1000 2 1000 2 1000 2 2 1000 1000 1000 22 1000 10 1000 1000 1000 1000 10 10 1000 1000 10 1000 1000 10 1000 10 23 1000 8 8 1000 1000 8 1000 1000 1000 1000 1000 8 8 1000 8 1000 24 9 1000 1000 9 1000 9 1000 1000 1000 1000 9 1000 9 1000 1000 9 25 1000 7 1000 7 1000 7 1000 1000 7 1000 7 1000 1000 7 1000 1000 26 1000 1000 6 6 1000 6 1000 6 6 1000 1000 1000 1000 1000 6 1000 27 1000 1000 8 8 1000 8 1000 8 8 1000 1000 1000 1000 1000 8 1000 28 3 1000 1000 3 3 1000 1000 3 1000 3 1000 1000 1000 1000 3 1000 29 1000 7 7 1000 1000 7 1000 1000 1000 1000 1000 7 7 1000 7 1000 30 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 31 6 1000 1000 1000 1000 1000 6 1000 6 1000 6 1000 1000 6 6 1000 32 2 1000 1000 2 1000 2 1000 1000 1000 1000 2 1000 2 1000 1000 2 33 1000 10 10 1000 1000 10 1000 1000 1000 1000 1000 10 10 1000 10 1000 34 1000 4 1000 1000 1000 1000 4 4 1000 1000 4 1000 1000 4 1000 4 35 1000 6 1000 6 1000 6 1000 1000 6 1000 6 1000 1000 6 1000 1000 36 5 1000 1000 1000 1000 1000 5 1000 5 1000 5 1000 1000 5 5 1000 37 1000 8 1000 1000 8 1000 1000 1000 8 1000 1000 8 1000 8 1000 8 38 1000 2 2 1000 1000 2 1000 1000 1000 1000 1000 2 2 1000 2 1000 39 1000 1000 4 1000 4 1000 4 1000 1000 4 1000 4 1000 1000 1000 4 40 6 1000 1000 6 1000 6 1000 1000 1000 1000 6 1000 6 1000 1000 6 41 8 1000 1000 8 8 1000 1000 8 1000 8 1000 1000 1000 1000 8 1000 42 1000 7 1000 1000 1000 1000 7 7 1000 1000 7 1000 1000 7 1000 7 43 1000 1000 3 1000 3 1000 1000 3 1000 3 1000 3 3 1000 1000 1000 44 1000 10 1000 10 1000 10 1000 1000 10 1000 10 1000 1000 10 1000 1000 45 2 1000 1000 1000 1000 1000 2 1000 2 1000 2 1000 1000 2 2 1000 46 1000 10 10 1000 1000 10 1000 1000 1000 1000 1000 10 10 1000 10 1000 47 3 1000 1000 1000 1000 1000 3 1000 3 1000 3 1000 1000 3 3 1000 48 8 1000 1000 8 1000 8 1000 1000 1000 1000 8 1000 8 1000 1000 8 49 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 50 5 1000 1000 5 5 1000 1000 5 1000 5 1000 1000 1000 1000 5 1000 51 1000 3 1000 1000 3 1000 1000 1000 3 1000 1000 3 1000 3 1000 3 52 6 1000 1000 6 1000 6 1000 1000 1000 1000 6 1000 6 1000 1000 6 53 1000 1000 4 4 1000 4 1000 4 4 1000 1000 1000 1000 1000 4 1000 54 1000 8 1000 1000 1000 1000 8 8 1000 1000 8 1000 1000 8 1000 8 55 1000 1000 5 1000 5 1000 5 1000 1000 5 1000 5 1000 1000 1000 5 56 1000 2 2 1000 1000 2 1000 1000 1000 1000 1000 2 2 1000 2 1000 57 1000 10 1000 10 1000 10 1000 1000 10 1000 10 1000 1000 10 1000 1000 58 6 1000 1000 6 6 1000 1000 6 1000 6 1000 1000 1000 1000 6 1000 59 5 1000 1000 1000 1000 1000 5 1000 5 1000 5 1000 1000 5 5 1000 60 1000 4 1000 1000 4 1000 1000 1000 4 1000 1000 4 1000 4 1000 4 61 1000 1000 8 8 1000 8 1000 8 8 1000 1000 1000 1000 1000 8 1000 62 5 1000 1000 5 1000 5 1000 1000 1000 1000 5 1000 5 1000 1000 5 63 2 1000 1000 2 2 1000 1000 2 1000 2 1000 1000 1000 1000 2 1000 64 10 1000 1000 1000 1000 1000 10 1000 10 1000 10 1000 1000 10 10 1000 65 1000 3 1000 1000 1000 1000 3 3 1000 1000 3 1000 1000 3 1000 3 | Predecessor Successor 1 3 2 3 3 5 4 5 6 7 7 8 5 9 8 9 10 12 11 12 13 16 14 16 15 16 12 17 16 17 18 19 19 20 21 22 22 23 24 25 20 26 23 26 25 26 27 28 28 29 29 30 30 31 31 32 33 35 34 35 36 38 37 38 35 39 38 39 40 41 42 43 41 44 43 44 44 45 46 47 48 49 47 50 49 50 51 52 52 53 53 54 54 55 55 56 57 58 58 59 59 60 61 63 62 63 63 65 64 65 | WorkStation Product Task Start_Time Completion_Time 1 P7 48 0 12 2 P9 57 0 11 2 P7 49 10 25 2 P5 34 14 25 2 P6 44 18 28 3 P7 46 1 7 3 P8 53 11 24 3 P2 16 21 28 3 P1 9 28 30 4 P3 24 1 8 4 P9 58 10 6 1 P1 4 16 13 4 P4 32 28 17 5 P3 21 0 18 5 P2 11 2 21 5 P4 28 8 27 5 P6 43 11 30 5 P10 63 14 5 5 P5 37 16 16 10 P1 5 25 21 6 P10 61 0 2 6 P2 14 8 12 6 P1 7 19 24 6 P3 26 24 10 7 P6 42 0 19 7 P2 13 8 30 7 P10 64 17 8 8 P4 27 0 11 8 P8 54 15 18 8 P1 8 24 22 9 P1 6 0 28 9 P5 36 7 30 9 P3 25 12 16 9 P5 35 19 18 9 P9 60 26 25 10 P2 10 0 12 10 P6 41 8 24 11 P6 40 0 26 11 P1 1 6 30 11 P3 20 17 6 11 P9 59 21 16 11 P2 17 27 7 12 P8 51 0 14 12 P1 2 3 28 12 P4 29 11 30 12 P4 30 18 11 12 P8 55 23 15 12 P8 56 28 8 13 P10 62 0 14 13 P5 33 6 21 13 P3 23 16 3 13 P5 38 24 11 14 P3 22 2 15 14 P7 47 12 23 14 P1 3 15 28 14 P10 65 27 30 15 P2 12 8 10 1 P3 19 13 16 15 P7 50 16 26 15 P4 31 22 30 15 P6 45 28 8 16 P3 18 0 5 16 P8 52 5 16 16 P2 15 14 27 16 P5 39 26 30 |
| Utilization Rate: |
|---|
| Makespan = 30 Ws1: Total_Time=20.0, Utilization=0.6667 Ws2: Total_Time=28.0, Utilization=0.9333 Ws3: Total_Time=22.0, Utilization=0.7333 Ws4: Total_Time=17.0, Utilization=0.5667 Ws5: Total_Time=22.0, Utilization=0.7333 Ws6: Total_Time=29.0, Utilization=0.9667 Ws7: Total_Time=26.0, Utilization=0.8667 Ws8: Total_Time=20.0, Utilization=0.6667 Ws9: Total_Time=29.0, Utilization=0.9667 Ws10: Total_Time=19.0, Utilization=0.6333 Ws11: Total_Time=24.0, Utilization=0.8000 Ws12: Total_Time=29.0, Utilization=0.9667 Ws13: Total_Time=25.0, Utilization=0.8333 Ws14: Total_Time=26.0, Utilization=0.8667 Ws15: Total_Time=18.0, Utilization=0.6000 Ws16: Total_Time=22.0, Utilization=0.7333 Average System Utilization: 0.7833 |
Makespan = 30 Run-time = 4456 seconds
Gantt Chart

